题目内容
设f(x,y,z)=
+
+
,其中x,y,z≥0,且x+y+z=1. 求f(x,y,z)的最大值和最小值.
| x(2y-z) |
| 1+x+3y |
| y(2z-x) |
| 1+y+3z |
| z(2x-y) |
| 1+z+3x |
分析:欲求f(x,y,z)的最大值和最小值,本题可转化为证明0≤f(x,y,z)≤
.利用柯西不等式,即可证得.
| 1 |
| 7 |
解答:解:先证f≤
,当且仅当x=y=z=
时等号成立.
因f=Σ
=1-2Σ
…(*)
由柯西不等式:Σ
≥
=
,
因为Σx(1+x+3y)=Σx(2x+4y+z)=2+Σxy≤
.
从而 Σ
≥
,f≤1-2×
=
,fmax=
,当且仅当x=y=z=
时等号成立.
再证f≥0,当x=1,y=z=0时等号成立.
事实上,f(x,y,z)=
+
+
=xy(
-
)+xz(
-
)+yz(
-
)=
+
+
≥0
故fmin=0,当x=1,y=z=0时等号成立.
故f(x,y,z)的最大值和最小值分别为
,0.
| 1 |
| 7 |
| 1 |
| 3 |
因f=Σ
| x(x+3y-1) |
| 1+x+3y |
| x |
| 1+x+3y |
由柯西不等式:Σ
| x |
| 1+x+3y |
| (Σx)2 |
| Σx(1+x+3y) |
| 1 |
| Σx(1+x+3y) |
因为Σx(1+x+3y)=Σx(2x+4y+z)=2+Σxy≤
| 7 |
| 3 |
从而 Σ
| x |
| 1+x+3y |
| 3 |
| 7 |
| 3 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 3 |
再证f≥0,当x=1,y=z=0时等号成立.
事实上,f(x,y,z)=
| x(2y-z) |
| 1+x+3y |
| y(2z-x) |
| 1+y+3z |
| z(2x-y) |
| 1+z+3x |
| 2 |
| 1+x+3y |
| 1 |
| 1+y+3z |
| 2 |
| 1+z+3x |
| 1 |
| 1+x+3y |
| 2 |
| 1+y+3z |
| 1 |
| 1+z+3x |
| 7xyz |
| (1+x+3y)(1+y+3z) |
| 7xyz |
| (1+z+3x)(1+x+3y) |
| 7xyz |
| (1+y+3z)(1+z+3x) |
故fmin=0,当x=1,y=z=0时等号成立.
故f(x,y,z)的最大值和最小值分别为
| 1 |
| 7 |
点评:本题考查柯西不等式,主要考查函数的最值,正确运用柯西不等式是关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
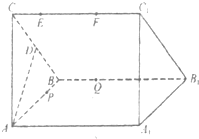 (2012•成都一模)设直三梭柱ABC-A1B1C1的底面为等腰直角三角形,AB=AC=2,动点E、F在侧棱CC1上,动点P、Q分别碰AB1,BB1上,若EF═1,CE=x,BQ=y,BP=z,其中x,y,z>0,则下列结论中错误的是.( )
(2012•成都一模)设直三梭柱ABC-A1B1C1的底面为等腰直角三角形,AB=AC=2,动点E、F在侧棱CC1上,动点P、Q分别碰AB1,BB1上,若EF═1,CE=x,BQ=y,BP=z,其中x,y,z>0,则下列结论中错误的是.( )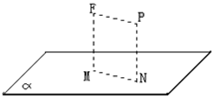 (2009•闸北区二模)和平面解析几何的观点相同,在空间中,空间曲面可以看作是适合某种条件的动点的轨迹.一般来说,在空间直角坐标系O-xyz中,空间曲面的方程是一个三元方程F(x,y,z)=0.
(2009•闸北区二模)和平面解析几何的观点相同,在空间中,空间曲面可以看作是适合某种条件的动点的轨迹.一般来说,在空间直角坐标系O-xyz中,空间曲面的方程是一个三元方程F(x,y,z)=0.