题目内容
已知在正方体ABCD－A′B′C′D′中，M、N分别是A′D′、A′B′的中点，在该正方体中是否存在过顶点且与平面AMN平行的平面？若存在，试作出该平面，并证明你的结论；若不存在，请说明理由．
[解析] 存在．与平面AMN平行的平面有以下三种情况(E、F分别为所在棱的中点)：
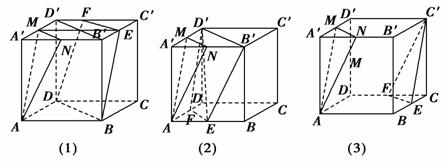
下面以图(1)为例进行证明．
∵四边形ABEM是平行四边形，∴BE∥AM，
又BE⊂平面BDE，AM⊄平面BDE，
∴AM∥平面BDFE.
∵MN是△A′B′D′的中位线，∴MN∥B′D′，
∵四边形BDD′B′是平行四边形，
∴BD∥B′D′，∴MN∥BD，
又BD⊂平面BDE，MN⊄平面BDE，
∴MN∥平面BDFE，
又AM⊂平面AMN，MN⊂平面AMN，且AM∩MN＝M，
∴由平面与平面平行的判定定理可得，平面AMN∥平面BDFE.
练习册系列答案
相关题目
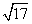，则该二面角的大小为( )
的正三棱锥V－ABC中，∠AVB＝∠BVC＝∠CVA＝40°，过点A作截面AEF，则截面△AEF周长的最小值为________．
[
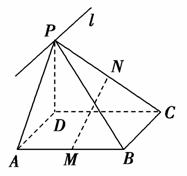B.