题目内容
过抛物线y2=2px(p>0)的焦点作倾斜角为θ的直线l,设l交抛物线于A、B两点,(1)求|AB|;(2)求|AB|的最小值.
思路分析:本题考查抛物线的焦点弦及通径问题.经过抛物线的焦点的直线方程我们可以设出来,然后联立该方程与抛物线的方程得到一个方程组,即可解得其关系.
解:(1)当θ=90°时,直线AB的方程为x=![]() .由
.由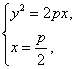
得A(![]() ,-p)、B(
,-p)、B(![]() ,p).∴|AB|=2p.
,p).∴|AB|=2p.
当θ≠90°时,直线AB的方程为y=(x-![]() )tanθ.由
)tanθ.由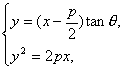
得tan2θ·x2-(2p+ptan2θ)x+![]() ·tan2θ=0.
·tan2θ=0.
设A(x1,y1)、B(x2,y2),则x1+x2=![]() ,
,
∴|AB|=x1+![]() +x2+
+x2+![]() =p+
=p+![]() =
=![]() .
.
(2)由(1)知,当θ=90°时,|AB|最小值为2p.
深化升华 求过抛物线焦点的弦长问题,一般是把弦分成两条焦半径,利用焦半径公式结合韦达定理来求,过焦点的最短弦(与对称轴垂直)是抛物线的通径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过抛物线y2=2px(p>0)的焦点F的直线l与抛物线在第一象限的交点为A,与抛物线的准线的交点为B,点A在抛物线准线上的射影为C,若
=
,
•
=48,则抛物线的方程为( )
| AF |
| FB |
| BA |
| BC |
| A、y2=4x | ||
| B、y2=8x | ||
| C、y2=16x | ||
D、y2=4
|
过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A、B两点,O为抛物线的顶点.则△ABO是一个( )
| A、等边三角形 | B、直角三角形 | C、不等边锐角三角形 | D、钝角三角形 |