Question

【题目】如图，已知菱形ABEF所在的平面与△ABC所在的平面相互垂直，AB=4，BC= ，BC⊥BE，∠ABE= ．

（1）求证：BC⊥平面ABEF；
（2）求平面ACF与平面BCE所成的锐二面角的余弦值．

Answer 1

【答案】
（1）

解：如图，在菱形ABEF中，取AB中点O，∵，∠ABE= ．∴EO⊥AB，

又∵平面ABEF⊥面ABC，平面ABEF∩面ABC=AB，EO面ABEF

∴．EO⊥面ABC，则EO⊥BC，又∵BC⊥BE，且BE∩EO=E

∴BC⊥平面ABEF

（2）

解：由（1）得EO⊥面ABC，BC⊥平面ABEF．

∴以O为原点，OB，OE所在直线为y、z轴建立如图直角坐标系O﹣xyz．

则A（0，﹣2，0），B（0，2，0），C（ ，2，0），F（0，﹣4，2 ），E（0，0，2 ）．

设平面ACF的法向量为 ，

，

由 取 ．

设平面BCE的法向量为 ，

， ，

由 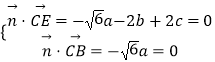，取 ．

，

∴平面ACF与平面BCE所成的锐二面角的余弦值为 ．

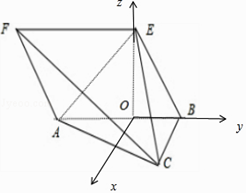
【解析】（1）如图，在菱形ABEF中，取AB中点O，可得EO⊥面ABC，EO⊥BC，BC⊥平面ABEF．（2）由（1）得EO⊥面ABC，BC⊥平面ABEF．以O为原点，OB，OE所在直线为y、z轴建立如图直角坐标系O﹣xyz．则A（0，﹣2，0），B（0，2，0），C（ ，2，0），F（0，﹣4，2 ），E（0，0，2 ）．
求出平面ACF的法向量为 ，平面BCE的法向量为 ，利用向量法夹角公式即可求解．
【考点精析】认真审题，首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)．