题目内容
已知函数f(x)＝ax＋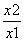
(a>1)，用反证法证明方程f(x)＝0没有负数根．
证明 假设方程f(x)＝0有负数根，设为x0(x0≠－1)．
则有x0<0，且f(x0)＝0.
∴ax0＋
＝0⇔ax0＝－.
∵a>1，∴0<ax0<1，
∴0<－<1.
解上述不等式，得
<x0<2.
这与假设x0<0矛盾．
故方程f(x)＝0没有负数根．
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
已知函数f(x)＝ax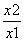＋ (a>1)，用反证法证明方程f(x)＝0没有负数根．
证明 假设方程f(x)＝0有负数根，设为x0(x0≠－1)．
则有x0<0，且f(x0)＝0.
∴ax0＋＝0⇔ax0＝－.
∵a>1，∴0<ax0<1，
∴0<－<1.
解上述不等式，得<x0<2.
这与假设x0<0矛盾．
故方程f(x)＝0没有负数根．
名校课堂系列答案
的边长为
，平面内一点
满足
，则
. 
.
a升，搅匀后再倒出溶液
(n＝1,2，…)，试证：“数列{xn}对任意的正整数n都满足xn>xn＋1”，当此题用反证法否定结论时应为____________________．
，
)的坐标公式
(其中A(x1，y1)、B(x2，y2)、C(x3，y3))，猜想以A(x1，y1，z1)、B(x2，y2，z2)、C(x3，y3，z3)、D(x4，y4，z4)为顶点的四面体A—BCD的重心G(
)的公式为________．
上述定理，写出对空间四面体性质的猜想．