题目内容
4.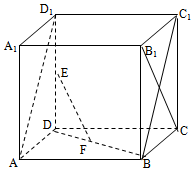 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、BD的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、BD的中点.(Ⅰ)求证:EF∥平面ABC1D1
(Ⅱ)求证:EF⊥B1C
(Ⅲ)求三棱锥A1-ABD1的体积.
分析 (Ⅰ)连结BD1,则EF∥D1B,由此能证明EF∥平面ABC1D1.
(Ⅱ)由B1C⊥AB,B1C⊥BC1,知B1C⊥平面ABC1D1,由此能证明EF⊥B1C.
(Ⅲ)三棱锥A1-ABD1的体积${V_{{A_1}-AB{D_1}}}={V_{{D_1}-{A_1}AB}}$,由此能求出结果.
解答 (本小题满分12分)
证明:(Ⅰ)连结BD1,
在△DD1B中,E、F分别为D1D,DB的中点,则EF∥D1B,
又∵D1B?平面ABC1D1,EF?平面ABC1D1,
∴EF∥平面ABC1D1.(3分)
(Ⅱ)∵B1C⊥AB,B1C⊥BC1,
AB?平面ABC1D1,BC1?平面ABC1D1,
AB∩BC1=B,
∴B1C⊥平面ABC1D1.
又∵BD1?平面ABC1D1,∴B1C⊥BD1,
而EF∥BD1,∴EF⊥B1C.(8分)
解:(Ⅲ)三棱锥A1-ABD1的体积:
${V_{{A_1}-AB{D_1}}}={V_{{D_1}-{A_1}AB}}$=$\frac{1}{3}×{S}_{△{A}_{1}AB}×{A}_{1}{D}_{1}$
=$\frac{1}{3}×\frac{1}{2}×A{A}_{1}×AB×{A}_{1}{D}_{1}$
=$\frac{1}{3}×\frac{1}{2}×2×2×2=\frac{4}{3}$.(12分)
点评 本题考查线面平行的证明,考查线线垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
15.曲线y=4-x3在点(-1,5)处的切线方程是( )
| A. | 3x+y-2=0 | B. | y=7x+2 | C. | y=x-4 | D. | y=7x+4 |
12.函数y=log3x(x≥1)的值域是( )
| A. | [2,+∞) | B. | (3,+∞) | C. | [0,+∞) | D. | R |
19.到两定点(-2,0),(2,0)的距离之差的绝对值为定值3的点的轨迹是( )
| A. | 椭圆 | B. | 线段 | C. | 直线 | D. | 双曲线 |
16.G为△ADE的重心,点P为△DEG内部(含边界)上任一点,B,C均为AD,AE上的三等分点(靠近点A),$\overrightarrow{AP}$=α$\overrightarrow{AB}$+β$\overrightarrow{AC}$(α,β∈R),则α+$\frac{1}{2}$β的范围是( )
| A. | [1,2] | B. | [1,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2] | D. | [$\frac{3}{2}$,3] |
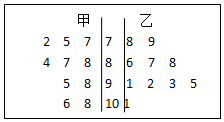 在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.
在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.