题目内容
已知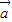 =(λ,2),
=(λ,2),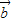 =(-3,5),且
=(-3,5),且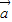 与
与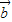 的夹角为钝角,则λ的取值范围是( )
的夹角为钝角,则λ的取值范围是( )A.λ>
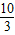
B.λ≥
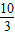
C.λ<
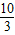
D.λ≤
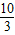
【答案】分析:根据两个向量的夹角是钝角,则两个向量的夹角的余弦小于零,从而得到两个向量的数量积小于零,用坐标形式表示向量的数量积,解不等式,得到变量的范围.
解答:解:∵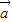 与
与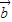 的夹角为钝角,
的夹角为钝角,
∴cos<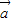 ,
,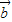 ><0.且
><0.且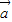 与
与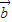 不共线
不共线
∴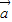 •
•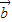 <0.且-3λ-10≠0
<0.且-3λ-10≠0
∴-3λ+10<0.且λ≠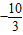
∴λ>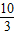 .
.
故选A
点评:两个向量的数量积是一个数量,它的值是两个向量的模与两向量夹角余弦的乘积,结果可正、可负、可以为零,其符号由夹角的余弦值确定.
解答:解:∵
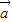 与
与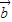 的夹角为钝角,
的夹角为钝角,∴cos<
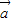 ,
,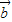 ><0.且
><0.且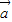 与
与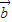 不共线
不共线∴
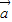 •
•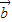 <0.且-3λ-10≠0
<0.且-3λ-10≠0∴-3λ+10<0.且λ≠
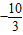
∴λ>
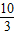 .
.故选A
点评:两个向量的数量积是一个数量,它的值是两个向量的模与两向量夹角余弦的乘积,结果可正、可负、可以为零,其符号由夹角的余弦值确定.

练习册系列答案
相关题目