题目内容
3.正方体的表面积为24,则该正方体的内切球的体积为$\frac{4π}{3}$.分析 由已知求出正方体的棱长为$\sqrt{\frac{24}{6}}$=2,所以正方体的内切球的直径为2,由球的体积公式得到所求.
解答 解:因为正方体的表面积为24,所以棱长为$\sqrt{\frac{24}{6}}$=2,所以正方体的内切球的直径为2,所以该正方体的内切球的体积为$\frac{4}{3}π×{1}^{3}=\frac{4π}{3}$;
故答案为:$\frac{4π}{3}$.
点评 本题考查了正方体的内切球体积的求法;关键是求出内切球的半径.

练习册系列答案
相关题目
13.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x+y-1≤0}\\{x-y-1≤0}\\{x≥0}\end{array}\right.$,则z=x+2y的最大值为( )
| A. | -2 | B. | 2 | C. | 1 | D. | -1 |
14.如图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.则①处可填写( )
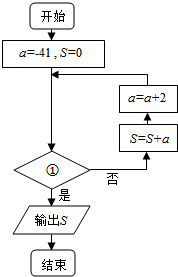

| A. | S>0 | B. | S<0 | C. | a>0 | D. | a=0 |
8.已知关于x的方程x2-(bcosA)x+acosB=0的两根之积等于两根之和,且边a,b为△ABC的两内角A,B所对的边,则△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
15.已知函数f(x)=ex-e-x(e=2.71828…)是自然对数的底数),f(x)的导数是( )
| A. | 偶函数 | B. | 奇函数 | C. | 增函数 | D. | 减函数 |
