题目内容
已知,分别为椭圆
+
=1(a>b>0)左、右焦点,B为椭圆短轴的一个端点,若
•
≥
,则椭圆离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| BF2 |
| 1 |
| 2 |
| F1F22 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
分析:先令B(0,b),则
=(-c,-b),
=(c,-b),
•
=b2-c2,由b2-c2≥
×4c2,构造出关于e的不等关系求离心率的取值范围即可.
| BF1 |
| BF2 |
| BF1 |
| BF2 |
| 1 |
| 2 |
解答:解:令B(0,b),则
=(-c,-b),
=(c,-b),
∴
•
=b2-c2,即b2-c2≥
×4c2,得a2≥4c2,
∴e≤
,故e∈(0,
],
故选:A.
| BF1 |
| BF2 |
∴
| BF1 |
| BF2 |
| 1 |
| 2 |
∴e≤
| 1 |
| 2 |
| 1 |
| 2 |
故选:A.
点评:本题考查椭圆的性质及其应用,难度不大,正确解题的关键是构造出关于e的不等关系求离心率的取值范围,同时要注意椭圆离心率的取值范围是(0,1).

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 如图,已知点P为椭圆
如图,已知点P为椭圆 (2012•奉贤区二模)已知:P为椭圆
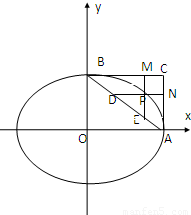
(2012•奉贤区二模)已知:P为椭圆 在第一象限内的任意一点,过椭圆的右顶点A和上顶点B分别作与y轴和x轴的平行线交于C,过P引BC、AC的平行线交AC于N,交BC于M,交AB于D、E,矩形PMCN的面积是S1,三角形PDE的面积是S2,则S1:S2= .
在第一象限内的任意一点,过椭圆的右顶点A和上顶点B分别作与y轴和x轴的平行线交于C,过P引BC、AC的平行线交AC于N,交BC于M,交AB于D、E,矩形PMCN的面积是S1,三角形PDE的面积是S2,则S1:S2= .
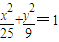 上的任意一点,过椭圆的右顶点A和上顶点B分别作与x轴和y 轴的平行线交于C,过P引BC、AC的平行线交AC于N,交BC于M,交AB于D、E,矩形PMCN是S1,三角形PDE的面积是S2,则S1:S2=( )
上的任意一点,过椭圆的右顶点A和上顶点B分别作与x轴和y 轴的平行线交于C,过P引BC、AC的平行线交AC于N,交BC于M,交AB于D、E,矩形PMCN是S1,三角形PDE的面积是S2,则S1:S2=( )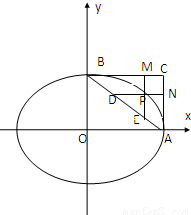

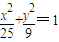 上的任意一点,过椭圆的右顶点A和上顶点B分别作与x轴和y 轴的平行线交于C,过P引BC、AC的平行线交AC于N,交BC于M,交AB于D、E,矩形PMCN是S1,三角形PDE的面积是S2,则S1:S2=( )
上的任意一点,过椭圆的右顶点A和上顶点B分别作与x轴和y 轴的平行线交于C,过P引BC、AC的平行线交AC于N,交BC于M,交AB于D、E,矩形PMCN是S1,三角形PDE的面积是S2,则S1:S2=( )