题目内容
已知函数 ,
, ,其中
,其中 .
.
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)若 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(Ⅲ)设函数 ,当
,当 时,若
时,若 ,
, ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 ,
, ,其中
,其中 .
.(Ⅰ)讨论
 的单调性;
的单调性;(Ⅱ)若
 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;(Ⅲ)设函数
 ,当
,当 时,若
时,若 ,
, ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围.(1)见解析;(2) ;(3)
;(3) .
.
 ;(3)
;(3) .
.试题分析:(1)求出
 ,然后根据
,然后根据 的符号讨论
的符号讨论 的单调性;(2)求出
的单调性;(2)求出 ,然后将条件转化为
,然后将条件转化为 ,
, .然后分离参数得到
.然后分离参数得到 ,然后用基本不等式求得
,然后用基本不等式求得 即可得到
即可得到 的取值范围;(3)将“若
的取值范围;(3)将“若 ,
, ,总有
,总有 成立”转化成“
成立”转化成“ 在
在 上的最大值不小于
上的最大值不小于 在
在 上的最大值”即可求得
上的最大值”即可求得 的取值范围.
的取值范围.试题解析:(1)
 的定义域为
的定义域为 ,且
,且 ,
,①当
 时,
时, ,
, 在
在 上单调递增;
上单调递增;②当
 时,由
时,由 ,得
,得 ;由
;由 ,得
,得 ;
;故
 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.(2)
 ,
, 的定义域为
的定义域为 .
. .
.因为
 在其定义域内为增函数,所以
在其定义域内为增函数,所以 ,
, .
. .
.而
 ,当且仅当
,当且仅当 时取等号,所以
时取等号,所以 .
.(3)当
 时,
时, ,
, .
.由
 得
得 或
或 .
.当
 时,
时, ;当
;当 时,
时, .
.所以在
 上,
上, .
.而“
 ,
, ,总有
,总有 成立”等价于“
成立”等价于“ 在
在 上的最大值不小于
上的最大值不小于 在
在 上的最大值”.
上的最大值”.而
 在
在 上的最大值为
上的最大值为 ,
,所以有
 .
.所以实数
 的取值范围是
的取值范围是 .
.
练习册系列答案
相关题目
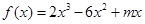
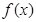 的解析表达式;
的解析表达式;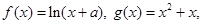 若函数
若函数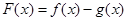 在x = 0处取得极值.
在x = 0处取得极值.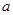 的值;
的值;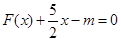 在区间[0,2]上恰有两个不同的实数根,求实数
在区间[0,2]上恰有两个不同的实数根,求实数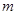 的取值范围;
的取值范围;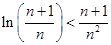 都成立.
都成立.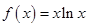 .
.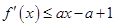 恒成立,求实数a的集合.
恒成立,求实数a的集合.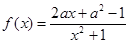 ,其中
,其中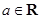 .
.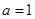 时,记
时,记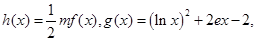 存在
存在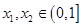 使
使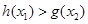 成立,求实数
成立,求实数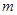 的取值范围;
的取值范围;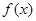 在
在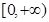 上存在最大值和最小值,求
上存在最大值和最小值,求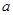 的取值范围.
的取值范围.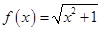 ,对任意
,对任意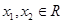 ,恒有
,恒有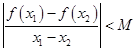 ,其中M是常数,则M的最小值是 .
,其中M是常数,则M的最小值是 .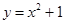 在点
在点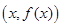 处的切线的斜率为
处的切线的斜率为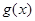 ,则函数
,则函数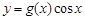 的部分图象可以为( )
的部分图象可以为( )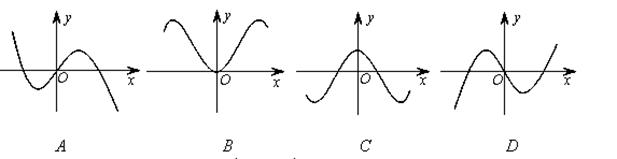
 及其导数
及其导数 ,若存在
,若存在 ,使得
,使得 =
= ,则称
,则称 是
是 ,②
,② ,③
,③ ,④
,④ ,⑤
,⑤
 ,其中
,其中 ,则
,则 是偶函数的充要条件是( )
是偶函数的充要条件是( )


