Question

（08年上虞市质量调测二理） 如图，平面ABCD⊥平面ABEF，ABCD是正方形，ABEF是矩形，G是线段EF的中点，且B点在平面ACG内的射影在CG上.

(I)求证：AG⊥平面BCG；

(II) 求直线BE与平面ACG所成角的大小.

 

 

Answer 1

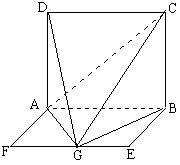
解法一：

 (I)过B作BH⊥面ACG于H，由已知，H在CG上，则BH⊥AG,

由于平面ABCD⊥平面ABEF，BC⊥AB.

所以 BC⊥平面ABEF,  BC⊥AG，

所以 AG⊥平面BCG；

（Ⅱ）法1

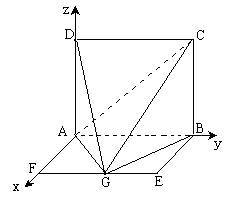
如图,以A为坐标原点,AF为x轴,AB为y轴,AD为z轴,建立空间直角坐标系。设正方形ABCD边长是1, 由（I）知，AG⊥平面BCG；，故AG⊥BG,

AF=BE= AB,

则A(0,0,0), G(,,0), C(0,1,1),

设面ACG的法向量为=(x,y,z)

则?=x+y=0

?=y+z=0

取x=1,得＝（1,－1,1）

而=(,0,0)

所以，cos<，>==

所以直线BE与平面ACG所成角为arcsin。

 

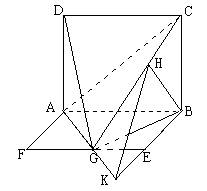
法2.

延长AG、BE交于K,连HK,

因为BH⊥面ACG

所以 ∠KHB即为直线BE与平面ACG所成角。

由（I）知，AG⊥平面BCG；，故AG⊥BG,

AF=BE= AB.

BG=AB,

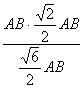BH===AB.

Sin∠KHB==.

所以直线BE与平面ACG所成角为arcsin.