��Ŀ����
 �����Ϊ����������{an}��ǰn���ΪSn������2��Sn+1��=an2+an��n��N*����
�����Ϊ����������{an}��ǰn���ΪSn������2��Sn+1��=an2+an��n��N*������1��������{an}��ͨ�ʽ��
��2��������{bn}����b1=2��bn+1=2bn��n��N*��������{cn}����cn=
|
��3��������Pn=
| 4 |
| 3 |
��������1��������֪a1=2��2an=an2-an-12+an-an-1����an��0��֪an-an-1=1�ɴ������an��
��2��������֪bn=2n��n��N*����nΪż��ʱ��Tn=��a1+a3+��+an-1��+��b2+b4+��+bn��=
+
=
+
(2n-1)��
��3���ɳ����֪��nΪż����Tn=
+
(2n-1)��Pn=
(2n-1)����dn=A-B=Tn-Pn=
��n=8ʱ��Tn-Pn=20����������ֹͣ����ͬѧ�Ĺ۵����
��2��������֪bn=2n��n��N*����nΪż��ʱ��Tn=��a1+a3+��+an-1��+��b2+b4+��+bn��=
(a1+an-1)•
| ||
| 2 |
4(1-4
| ||
| 1-4 |
| n2+2n |
| 4 |
| 4 |
| 3 |
��3���ɳ����֪��nΪż����Tn=
| n2+2n |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| n2+2n |
| 4 |
����⣺��1��n=1��2��S1+1��=a12+a1?a1=2����2�֣�
��
��ʽ�������2an=an2-an-12+an-an-1
��an��0����an-an-1=1����4�֣�
?{an}Ϊ�Ȳ����У�����Ϊ2������Ϊ1
��an=n+1��n��N*������5�֣�
��2����{bn}������Ϊ2������Ϊ2�ĵȱ����У�
��bn=2n��n��N*������7�֣�
nΪż��ʱ��Tn=��a1+a3+��+an-1��+��b2+b4+��+bn������8�֣�
=
+
=
+
(2n-1)����10�֣�
��3���ɳ����֪��nΪż����
��Tn=
+
(2n-1)��Pn=
(2n-1)
��dn=A-B=Tn-Pn=
����13�֣�
��n=8ʱ��
=20����nΪż��
��n=8ʱ��Tn-Pn=20����������ֹͣ����14�֣�
����ͬѧ�Ĺ۵����16�֣�
|
��ʽ�������2an=an2-an-12+an-an-1
��an��0����an-an-1=1����4�֣�
?{an}Ϊ�Ȳ����У�����Ϊ2������Ϊ1
��an=n+1��n��N*������5�֣�
��2����{bn}������Ϊ2������Ϊ2�ĵȱ����У�
��bn=2n��n��N*������7�֣�
nΪż��ʱ��Tn=��a1+a3+��+an-1��+��b2+b4+��+bn������8�֣�
=
(a1+an-1)•
| ||
| 2 |
4(1-4
| ||
| 1-4 |
| n2+2n |
| 4 |
| 4 |
| 3 |
��3���ɳ����֪��nΪż����
��Tn=
| n2+2n |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
��dn=A-B=Tn-Pn=
| n2+2n |
| 4 |
��n=8ʱ��
| n2+2n |
| 4 |
��n=8ʱ��Tn-Pn=20����������ֹͣ����14�֣�
����ͬѧ�Ĺ۵����16�֣�
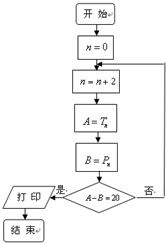
���������⿼������ͨ�ʽ��������ǰn��͵ļ��㷽�����Գ���ͼΪ���忼�����е����ʺ�Ӧ�ã�����ʱҪ�������⣬��ϸ���

��ϰ��ϵ�д�
 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�
�����Ŀ