题目内容
以O为原点, 所在直线为x轴,建立直角坐标系.设
所在直线为x轴,建立直角坐标系.设 ,点F的坐标为(t,0),t∈[3,+∞).点G的坐标为(x,y).
,点F的坐标为(t,0),t∈[3,+∞).点G的坐标为(x,y).(1)求x关于t的函数x=f(t)的表达式,并判断函数f(x)的单调性.
(2)设△OFG的面积
 ,若O以为中心,F,为焦点的椭圆经过点G,求当
,若O以为中心,F,为焦点的椭圆经过点G,求当 取最小值时椭圆的方程.
取最小值时椭圆的方程.(3)在(2)的条件下,若点P的坐标为
 ,C,D是椭圆上的两点,
,C,D是椭圆上的两点, ,求实数λ的取值范围.
,求实数λ的取值范围.
【答案】分析:(1)由F的坐标(t,0),.点G的坐标(x,y)可求出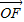 ,
,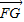 坐标,再代入
坐标,再代入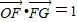 ,即可求x关于t的函数x=f(t)的表达式,再利用对勾函数的单调性判断函数f(x)的单调性.
,即可求x关于t的函数x=f(t)的表达式,再利用对勾函数的单调性判断函数f(x)的单调性.
(2)先用含点G的坐标式子表示△OFG的面积,再根据△OFG的面积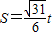 ,求出y0,再判断何时
,求出y0,再判断何时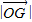 取最小值,
取最小值,
可得此时的椭圆方程.
(3)设C,D的坐标分别为(x,y)、(m,n),求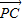 ,
,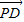 坐标,再根据
坐标,再根据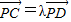 用含λ的式子表示n,根据n的范围求λ的范围即可.
用含λ的式子表示n,根据n的范围求λ的范围即可.
解答:解:(1)由题意得: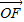 =(t,0),
=(t,0),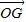 =(x,y),
=(x,y),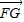 ═(x-t,y),
═(x-t,y),
则: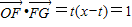 ,解得:
,解得: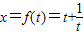
所以f(t)在t∈[3,+∞)上单调递增.
(2)由S= |
|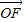 |•|y|=
|•|y|= |y|•t=
|y|•t=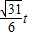 得y=±
得y=±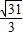 ,
,
点G的坐标为(t+ ,
,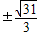 ),
),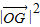 =
=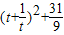
当t=3时,|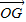 |取得最小值,此时点F,G的坐标为(3,0)、(
|取得最小值,此时点F,G的坐标为(3,0)、(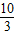 ,±
,±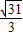 )
)
由题意设椭圆的方程为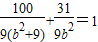 ,又点G在椭圆上,
,又点G在椭圆上,
解得b2=9或b2=-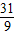 (舍)故所求的椭圆方程为
(舍)故所求的椭圆方程为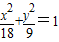
(3)设C,D的坐标分别为(x,y)、(m,n)
则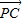 =(x,y-
=(x,y- ),
),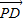 =(m,n-
=(m,n- )由
)由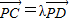 得(x,y-
得(x,y- )=λ=(m,n-
)=λ=(m,n- ),
),
∴x=λm,y=λn- λ+
λ+
又点C,D在椭圆上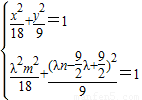 消去m得n=
消去m得n=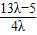
|n|≤3,∴|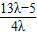 |≤3解得
|≤3解得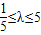
又∵λ≠1
∴实数λ的范围是[ ,1)∪(1,5]
,1)∪(1,5]
点评:本题考查了圆锥曲线与函数之间的关系,做题时要认真分析,找到之间的联系.
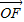 ,
,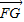 坐标,再代入
坐标,再代入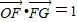 ,即可求x关于t的函数x=f(t)的表达式,再利用对勾函数的单调性判断函数f(x)的单调性.
,即可求x关于t的函数x=f(t)的表达式,再利用对勾函数的单调性判断函数f(x)的单调性.(2)先用含点G的坐标式子表示△OFG的面积,再根据△OFG的面积
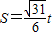 ,求出y0,再判断何时
,求出y0,再判断何时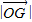 取最小值,
取最小值,可得此时的椭圆方程.
(3)设C,D的坐标分别为(x,y)、(m,n),求
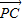 ,
,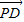 坐标,再根据
坐标,再根据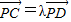 用含λ的式子表示n,根据n的范围求λ的范围即可.
用含λ的式子表示n,根据n的范围求λ的范围即可.解答:解:(1)由题意得:
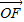 =(t,0),
=(t,0),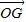 =(x,y),
=(x,y),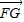 ═(x-t,y),
═(x-t,y),则:
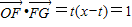 ,解得:
,解得: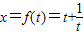
所以f(t)在t∈[3,+∞)上单调递增.
(2)由S=
 |
|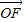 |•|y|=
|•|y|= |y|•t=
|y|•t=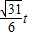 得y=±
得y=±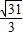 ,
,点G的坐标为(t+
 ,
,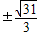 ),
),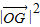 =
=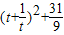
当t=3时,|
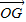 |取得最小值,此时点F,G的坐标为(3,0)、(
|取得最小值,此时点F,G的坐标为(3,0)、(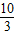 ,±
,±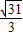 )
)由题意设椭圆的方程为
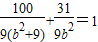 ,又点G在椭圆上,
,又点G在椭圆上,解得b2=9或b2=-
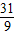 (舍)故所求的椭圆方程为
(舍)故所求的椭圆方程为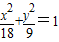
(3)设C,D的坐标分别为(x,y)、(m,n)
则
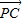 =(x,y-
=(x,y- ),
),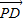 =(m,n-
=(m,n- )由
)由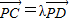 得(x,y-
得(x,y- )=λ=(m,n-
)=λ=(m,n- ),
),∴x=λm,y=λn-
 λ+
λ+
又点C,D在椭圆上
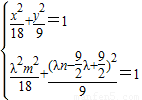 消去m得n=
消去m得n=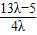
|n|≤3,∴|
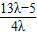 |≤3解得
|≤3解得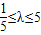
又∵λ≠1
∴实数λ的范围是[
 ,1)∪(1,5]
,1)∪(1,5]点评:本题考查了圆锥曲线与函数之间的关系,做题时要认真分析,找到之间的联系.

练习册系列答案
相关题目

 以O为原点,
以O为原点, 所在直线为x轴,建立如图所示的直角坐标系.若
所在直线为x轴,建立如图所示的直角坐标系.若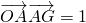 ,点A的坐标为(t,0),t∈(0,+∞),点G的坐标为(m,3).
,点A的坐标为(t,0),t∈(0,+∞),点G的坐标为(m,3).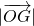 取最小值时双曲线C的方程;
取最小值时双曲线C的方程;