题目内容
设△ABC的内角A、B、C所对的边分别为a、b、c。已知a=1,b=2,cosC=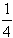 。
。
(1)求△ABC的周长;
(2)求cos(A-C)的值。
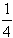 。
。(1)求△ABC的周长;
(2)求cos(A-C)的值。
解:(1)∵ c2=a2+b2-2abcosC=1+4-4×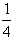 =4
=4
∴c=2
∴△ABC的周长为a+b+c=1+2+2=5。
(2)∵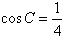
∴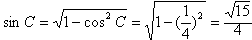
∴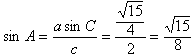
∵a<c,
∴A<C,故A为锐角
∴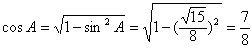
∴cos(A-C)=cosAcosC+sinAsinC=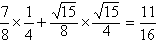 。
。
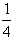 =4
=4∴c=2
∴△ABC的周长为a+b+c=1+2+2=5。
(2)∵
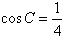
∴
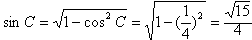
∴
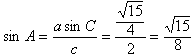
∵a<c,
∴A<C,故A为锐角
∴
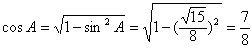
∴cos(A-C)=cosAcosC+sinAsinC=
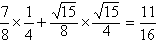 。
。
练习册系列答案
相关题目