题目内容
 已知方向向量为v=(1,
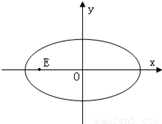
已知方向向量为v=(1, )的直线l过点(0,-2
)的直线l过点(0,-2 )和椭圆C:
)和椭圆C: +
+ =1(a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
=1(a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在过点E(-2,0)的直线m交椭圆C于点M、N,满足
 •
• =
= .cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
.cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
【答案】分析:(I)解法一:直线l:y= x-2
x-2 ,过原点垂直l的直线方程为y=-
,过原点垂直l的直线方程为y=- x,这两个方程联立可知x=
x,这两个方程联立可知x= .再由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,可知
.再由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,可知 =3.由此可以求出椭圆C的方程.
=3.由此可以求出椭圆C的方程.
解法二:直线l:y= x-3
x-3 .设原点关于直线l对称点为(p,q),则
.设原点关于直线l对称点为(p,q),则 解得p=3.由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,知
解得p=3.由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,知 =3.由此能够推出椭圆C的方程.
=3.由此能够推出椭圆C的方程.
(II)解:设M(x1,y1),N(x2,y2).当直线m不垂直x轴时,直线m:y=k(x+2)代入 +
+ =1,整理得(3k2+1)x2+12k2x+12k2-6=0,再由根与系数的关系和点到直线 的距离求解.
=1,整理得(3k2+1)x2+12k2x+12k2-6=0,再由根与系数的关系和点到直线 的距离求解.
解答:解:(I)解法一:直线l:y= x-2
x-2 ,①
,①
过原点垂直l的直线方程为y=- x,②
x,②
解①②得x= .
.
∵椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,∴ =2×
=2× =3.
=3.
∵直线l过椭圆焦点,∴该焦点坐标为(2,0).∴c=2,a2=6,b2=2.故椭圆C的方程为 +
+ =1③
=1③
解法二:直线l:y= x-3
x-3 .
.
设原点关于直线l对称点为(p,q),则 解得p=3.
解得p=3.
∵椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,∴ =3.
=3.
∵直线l过椭圆焦点,∴该焦点坐标为(2,0).∴c=2,a2=6,b2=2.故椭圆C的方程为 +
+ =1③
=1③
 (II)解:设M(x1,y1),N(x2,y2).
(II)解:设M(x1,y1),N(x2,y2).
当直线m不垂直x轴时,直线m:y=k(x+2)代入③,
整理得(3k2+1)x2+12k2x+12k2-6=0,
∴x1+x2=- ,x1•x2=
,x1•x2= ,
,
|MN|= =
= =
= ,
,
点O到直线MN的距离d=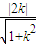 .
.
∵ •
• =
= cot∠MON,即|
cot∠MON,即| |•|
|•| |cos∠MON=
|cos∠MON= ≠0,
≠0,
∴| |•|
|•|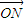 |sin∠MON=4
|sin∠MON=4 ,∴S△OMN=
,∴S△OMN= .∴|MN|•d=
.∴|MN|•d= ,
,
即4 |k|
|k| =
= (3k2+1),
(3k2+1),
整理得k2= ,∴k=±
,∴k=± .
.
 当直线m垂直x轴时,也满足S△OMN=
当直线m垂直x轴时,也满足S△OMN=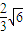 .
.
故直线m的方程为y= x+
x+ ,或y=-
,或y=-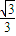 x-
x- ,或x=-2.
,或x=-2.
经检验上述直线均满足 •
• ≠0.
≠0.
所以所求直线方程为y= x+
x+ ,或y=-
,或y=- x-
x- ,或x=-2.
,或x=-2.
点评:本题综合考查直线的椭圆的位置关系,具有一定的难度,解题时要注意培养运算能力.
 x-2
x-2 ,过原点垂直l的直线方程为y=-
,过原点垂直l的直线方程为y=- x,这两个方程联立可知x=
x,这两个方程联立可知x= .再由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,可知
.再由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,可知 =3.由此可以求出椭圆C的方程.
=3.由此可以求出椭圆C的方程.解法二:直线l:y=
 x-3
x-3 .设原点关于直线l对称点为(p,q),则
.设原点关于直线l对称点为(p,q),则 解得p=3.由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,知
解得p=3.由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,知 =3.由此能够推出椭圆C的方程.
=3.由此能够推出椭圆C的方程.(II)解:设M(x1,y1),N(x2,y2).当直线m不垂直x轴时,直线m:y=k(x+2)代入
 +
+ =1,整理得(3k2+1)x2+12k2x+12k2-6=0,再由根与系数的关系和点到直线 的距离求解.
=1,整理得(3k2+1)x2+12k2x+12k2-6=0,再由根与系数的关系和点到直线 的距离求解.解答:解:(I)解法一:直线l:y=
 x-2
x-2 ,①
,①过原点垂直l的直线方程为y=-
 x,②
x,②解①②得x=
 .
.∵椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,∴
 =2×
=2× =3.
=3.∵直线l过椭圆焦点,∴该焦点坐标为(2,0).∴c=2,a2=6,b2=2.故椭圆C的方程为
 +
+ =1③
=1③解法二:直线l:y=
 x-3
x-3 .
.设原点关于直线l对称点为(p,q),则
 解得p=3.
解得p=3.∵椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,∴
 =3.
=3.∵直线l过椭圆焦点,∴该焦点坐标为(2,0).∴c=2,a2=6,b2=2.故椭圆C的方程为
 +
+ =1③
=1③ (II)解:设M(x1,y1),N(x2,y2).
(II)解:设M(x1,y1),N(x2,y2).当直线m不垂直x轴时,直线m:y=k(x+2)代入③,
整理得(3k2+1)x2+12k2x+12k2-6=0,
∴x1+x2=-
 ,x1•x2=
,x1•x2= ,
,|MN|=
 =
= =
= ,
,点O到直线MN的距离d=
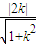 .
.∵
 •
• =
= cot∠MON,即|
cot∠MON,即| |•|
|•| |cos∠MON=
|cos∠MON= ≠0,
≠0,∴|
 |•|
|•|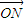 |sin∠MON=4
|sin∠MON=4 ,∴S△OMN=
,∴S△OMN= .∴|MN|•d=
.∴|MN|•d= ,
,即4
 |k|
|k| =
= (3k2+1),
(3k2+1),整理得k2=
 ,∴k=±
,∴k=± .
. 当直线m垂直x轴时,也满足S△OMN=
当直线m垂直x轴时,也满足S△OMN=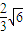 .
.故直线m的方程为y=
 x+
x+ ,或y=-
,或y=-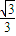 x-
x- ,或x=-2.
,或x=-2.经检验上述直线均满足
 •
• ≠0.
≠0.所以所求直线方程为y=
 x+
x+ ,或y=-
,或y=- x-
x- ,或x=-2.
,或x=-2.点评:本题综合考查直线的椭圆的位置关系,具有一定的难度,解题时要注意培养运算能力.

练习册系列答案
相关题目
 已知方向向量为v=(1,
已知方向向量为v=(1,