题目内容
在海岛A上有一座海拔1km的山峰,山顶设有一个观察站P,有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东15°、俯角为30°的B 处,到11:10时,又测得该船在岛北偏西45°、俯角为60°的C处。
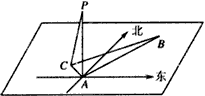
(1)求船的航行速度;
(2)求船从B到C行驶过程中与观察站P的最短距离。
(2)求船从B到C行驶过程中与观察站P的最短距离。
解:(1)设船速为xkm/h,则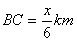
在Rt△PAB中,∠PBA与俯角相等为30°,
∴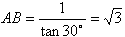
同理,Rt△PCA中,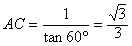
在△ACB中,∠CAB=15°+45°=60°
∴由余弦定理得,
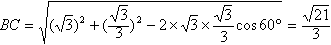
∴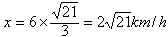
船的航行速度为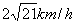 。
。
(2)由(1)知在△ACB中,由正弦定理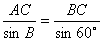
∴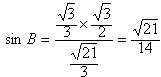
作AD⊥BC于点D,
∴当船行驶到点D时,AD最小,从而PD最小
此时,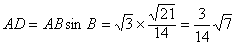
∴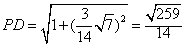
∴船在行驶过程中与观察站P的最短距离为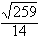 。
。
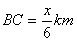
在Rt△PAB中,∠PBA与俯角相等为30°,
∴
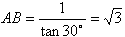
同理,Rt△PCA中,
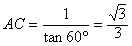
在△ACB中,∠CAB=15°+45°=60°
∴由余弦定理得,
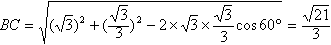
∴
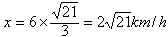
船的航行速度为
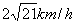 。
。(2)由(1)知在△ACB中,由正弦定理
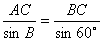
∴
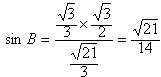
作AD⊥BC于点D,
∴当船行驶到点D时,AD最小,从而PD最小
此时,
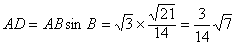
∴
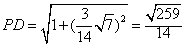
∴船在行驶过程中与观察站P的最短距离为
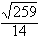 。
。
练习册系列答案
相关题目
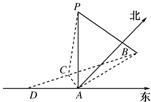 如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.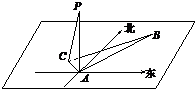 在海岛A上有一座海拔1km的山峰,山顶设有一个观察站P.有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东15°、俯角为30°的B处,到11:10时,又测得该船在岛北偏西45°、俯角为60°的C处.
在海岛A上有一座海拔1km的山峰,山顶设有一个观察站P.有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东15°、俯角为30°的B处,到11:10时,又测得该船在岛北偏西45°、俯角为60°的C处.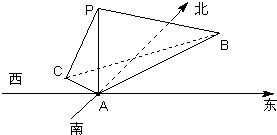 在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时,测得一轮船在岛北偏东30°、俯角为30°的B处,到9时10分又测得该船在岛北西60°、俯角为45°的C处.
在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时,测得一轮船在岛北偏东30°、俯角为30°的B处,到9时10分又测得该船在岛北西60°、俯角为45°的C处.