题目内容
10.判断下列函数的奇偶性:(1)f(x)=$\frac{(1+{2}^{x})^{2}}{{2}^{x}}$;
(2)f(x)=lg(x+$\sqrt{{x}^{2}+1}$);
(3)f(x)=lgx2+lg$\frac{1}{{x}^{2}}$.
分析 根据函数奇偶性的定义进行判断即可.
解答 解:(1)f(x)=$\frac{(1+{2}^{x})^{2}}{{2}^{x}}$=$\frac{1+2•{2}^{x}+{2}^{2x}}{{2}^{x}}$=$\frac{1}{{2}^{x}}$+2+2x,
则f(-x)=$\frac{1}{{2}^{x}}$+2+2x=f(x),则函数f(x)为偶函数;
(2)∵f(x)=lg(x+$\sqrt{{x}^{2}+1}$);
∴f(-x)+f(x)=lg(x+$\sqrt{{x}^{2}+1}$)+lg(-x+$\sqrt{{x}^{2}+1}$)=lg(x+$\sqrt{{x}^{2}+1}$)(-x+$\sqrt{{x}^{2}+1}$)=lg(x2+1-x2)=lg1=0,
即f(-x)=-f(x),则函数f(x)为奇函数.
(3)函数的定义域为(-∞,0)∪(0,+∞),
则f(-x)=lgx2+lg$\frac{1}{{x}^{2}}$=f(x),则函数f(x)为偶函数.
点评 本题主要考查函数奇偶性的判断,根据函数奇偶性的定义是解决本题的关键.

练习册系列答案
相关题目
5.已知公差不为0的等差数列{an}满足a1,a3,a4成等比数列,Sn为{an}的前n项和,则$\frac{{{S_3}-{S_2}}}{{{S_5}-{S_3}}}$的值为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{5}$ | D. | 4 |
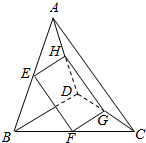 如图,三棱锥A-BCD中,AB=BC=CD=DA=BD=AC=2a,E,F,G,H分别是AB,BC,CD,DA的中点.
如图,三棱锥A-BCD中,AB=BC=CD=DA=BD=AC=2a,E,F,G,H分别是AB,BC,CD,DA的中点.