题目内容
5.已知公差不为0的等差数列{an}满足a1,a3,a4成等比数列,Sn为{an}的前n项和,则$\frac{{{S_3}-{S_2}}}{{{S_5}-{S_3}}}$的值为( )| A. | 2 | B. | 3 | C. | $\frac{1}{5}$ | D. | 4 |
分析 由a1,a3,a4成等比数列,利用等差数列的通项公式求出a1=-4d,由此利用等差数列的前n项和公式能求出$\frac{{{S_3}-{S_2}}}{{{S_5}-{S_3}}}$的值.
解答 解:设等差数列{an}的首项为a1,公差为d(d≠0),
因为a1,a3,a4成等比数列,
所以${a_1}{a_4}=a_3^2$,即a1=-4d,
所以$\frac{{{S_3}-{S_2}}}{{{S_5}-{S_3}}}=\frac{a_3}{{{a_5}+{a_4}}}=\frac{{{a_1}+2d}}{{2a_1^{\;}+7d}}=2$.
故选:A.
点评 本题考查等差数列的性质的应用,是基础题,解题时要注意等差数列的通项公式和前n项和公式的合理运用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
17.若输出的i=5,则k的最小正整数值为( )
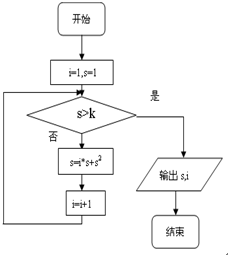

| A. | 88 | B. | 89 | C. | 8095 | D. | 8096 |
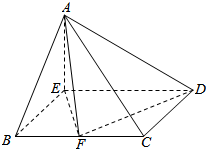 如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.
如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.