题目内容
求sin(-1 200°)·cos1 290°+cos(-1 020°)·sin(-1 050°)+tan945°的值.
解:原式=-sin(3×360°+120°)·cos(3×360°+210°)-cos(2×360°+300°)·sin(2×360°+330°) +tan(2×360°+225°)
=-sin(180°-60°)·cos(180°+30°)-cos(360°-60°)sin(360°-30°)+tan(180°+45°)
=sin60°·cos30°+cos60°·sin30°+tan45°
=![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
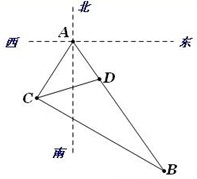 某观测站C在A城的南偏西20°方向上,由A城出发有一条公路走向是南偏东40°,测得距C点31千米的B处有一人正沿公路向A城走去,走了20千米后到达D处,此时C、D间的距离为21千米.
某观测站C在A城的南偏西20°方向上,由A城出发有一条公路走向是南偏东40°,测得距C点31千米的B处有一人正沿公路向A城走去,走了20千米后到达D处,此时C、D间的距离为21千米.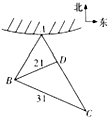 如图,某海滨城市位于海岸A处,在城市A的南偏西20°方向有一个海面观测站B,现测得与B处相距31海里的C处,有一艘豪华游轮正沿北偏西40°方向,以40海里/小时的速度向城市A直线航行,30分钟后到达D处,此时测得B、D间的距离为21海里.
如图,某海滨城市位于海岸A处,在城市A的南偏西20°方向有一个海面观测站B,现测得与B处相距31海里的C处,有一艘豪华游轮正沿北偏西40°方向,以40海里/小时的速度向城市A直线航行,30分钟后到达D处,此时测得B、D间的距离为21海里.