题目内容
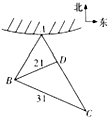 如图,某海滨城市位于海岸A处,在城市A的南偏西20°方向有一个海面观测站B,现测得与B处相距31海里的C处,有一艘豪华游轮正沿北偏西40°方向,以40海里/小时的速度向城市A直线航行,30分钟后到达D处,此时测得B、D间的距离为21海里.
如图,某海滨城市位于海岸A处,在城市A的南偏西20°方向有一个海面观测站B,现测得与B处相距31海里的C处,有一艘豪华游轮正沿北偏西40°方向,以40海里/小时的速度向城市A直线航行,30分钟后到达D处,此时测得B、D间的距离为21海里.(1)求sin∠BDC的值;
(2)试问这艘游轮再向前航行多少分钟即可到达城市A?
分析:(1)由已知可得 CD=20,△BDC中,根据余弦定理求得 cos∠BDC 的值,再利用同角三角函数的基本关系求得sin∠BDC 的值.
(2)由已知可得∠BAD=60°,由此可得sin∠ABD=sin(∠BDC-60°)的值,再由正弦定理求得 AD的值,由此求得这艘游轮到达A的时间.
(2)由已知可得∠BAD=60°,由此可得sin∠ABD=sin(∠BDC-60°)的值,再由正弦定理求得 AD的值,由此求得这艘游轮到达A的时间.
解答:解:(1)由已知可得 CD=40×
=20,△BDC中,根据余弦定理求得 cos∠BDC=
=-
,
∴sin∠BDC=
=
.
(2)由已知可得∠BAD=20°+40°=60°,∴sin∠ABD=sin(∠BDC-60°)=
×
-(-
)×
=
.
△ABD中,由正弦定理可得
=
.
又BD=21,∴AD=
=15,
∴t=
×60=22.5分钟.
即 这艘游轮再向前航行22.5分钟即可到达城市A.
| 1 |
| 2 |
| 212+ 202-31 2 |
| 2×21×20 |
| 1 |
| 7 |
∴sin∠BDC=
1-(-
|
4
| ||
| 7 |
(2)由已知可得∠BAD=20°+40°=60°,∴sin∠ABD=sin(∠BDC-60°)=
4
| ||
| 7 |
| 1 |
| 2 |
| 1 |
| 7 |
| ||
| 2 |
5
| ||
| 14 |
△ABD中,由正弦定理可得
| AD |
| sin∠ABD |
| BD |
| sin∠BAD |
又BD=21,∴AD=
| BD×sin∠ABD |
| sin∠BAD |
∴t=
| 15 |
| 40 |
即 这艘游轮再向前航行22.5分钟即可到达城市A.
点评:本题主要考查正弦定理和余弦定理的应用,同角三角函数的基本关系的应用,两角和差的正弦公式公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
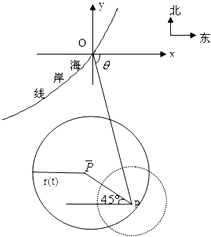 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南 某海滨城市坐落在一个三角形海域的顶点O处(如图),一条海岸线AO在城市O的正东方向,另一条海岸线OB在城市O北偏东
某海滨城市坐落在一个三角形海域的顶点O处(如图),一条海岸线AO在城市O的正东方向,另一条海岸线OB在城市O北偏东 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南 