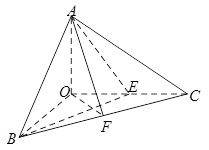
题目内容
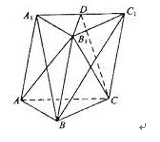
如图,已知三棱锥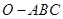 的侧棱
的侧棱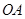 、
、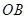 、
、 两两垂直,且
两两垂直,且 ,
,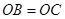
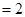 ,
, 是
是 的中点.
的中点.
(1)求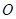 点到面
点到面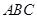 的距离;
的距离;
(2)求二面角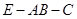 的正弦值.
的正弦值.
(1) ;(2)
;(2)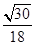 .
.
解析试题分析:(1)解法一是利用等体积法求出点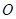 到平面
到平面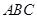 的距离,具体做法是:先利用
的距离,具体做法是:先利用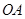 、
、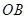 、
、 两两垂直以及它们的长度计算出三棱锥
两两垂直以及它们的长度计算出三棱锥 的体积,然后将此三棱锥转换成以点
的体积,然后将此三棱锥转换成以点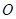 为顶点,以
为顶点,以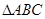 所在平面为底面的三棱锥通过体积来计算点
所在平面为底面的三棱锥通过体积来计算点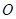 到平面
到平面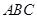 的距离;解法二是直接利用空间向量法求点
的距离;解法二是直接利用空间向量法求点 到平面
到平面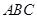 的距离;(2)解法一是通过三垂线法求二面角
的距离;(2)解法一是通过三垂线法求二面角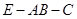 的正弦值,即
的正弦值,即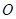 在平面
在平面 内作
内作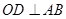 ,垂足为点
,垂足为点 ,连接
,连接 、
、 ,证明
,证明 ,
,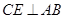 ,从而得到
,从而得到 为二面角
为二面角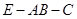 的平面角,再选择合适的三角形求出
的平面角,再选择合适的三角形求出 的正弦值;解法二是直接利用空间向量法求二面角
的正弦值;解法二是直接利用空间向量法求二面角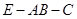 的余弦值,进而求出它的正弦值.
的余弦值,进而求出它的正弦值.
试题解析:解法一:(1)如下图所示,取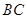 的中点
的中点 ,连接
,连接 、
、 ,
,
由于 ,
,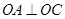 ,且
,且 ,
,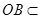 平面
平面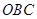 ,
, 平面
平面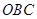 ,
, 平面
平面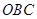 ,
, 平面
平面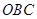 ,
, ,
, ,
,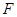 为
为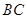 的中点,
的中点,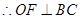 ,
,  ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,
, ,
, ,且
,且 ,
, ,
, 为
为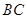 的中点,
的中点,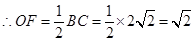 ,
, 平面
平面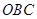 ,
, 平面
平面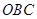 ,
,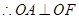 ,
, ,
, ,
,
而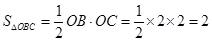 ,
,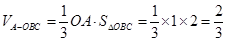 ,
,
设点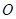 到平面
到平面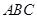 的距离为
的距离为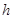 ,由等体积法知,
,由等体积法知, ,
,
即
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
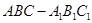 中,
中,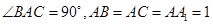 ,
,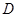 是棱
是棱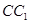 上的一点,
上的一点,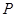 是
是 的延长线与
的延长线与 的延长线的交点,且
的延长线的交点,且 ∥平面
∥平面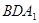 。
。
 ;
; 的平面角的余弦值;
的平面角的余弦值; 到平面
到平面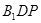 的距离.
的距离.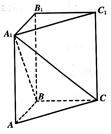
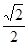 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离. 的侧面
的侧面 是菱形,
是菱形,
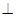 平面
平面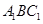 ;
;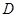 是
是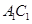 上的点,且
上的点,且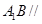 平面
平面 ,求
,求 的值.
的值.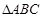 与
与 所在平面互相垂直,且
所在平面互相垂直,且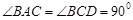 ,
,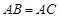 ,
,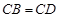 ,点
,点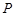 ,
, 分别在线段
分别在线段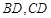 上,沿直线
上,沿直线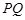 将
将
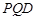 向上翻折,使
向上翻折,使 与
与 重合.
重合.
 ;
; 与平面
与平面 所成的角的正弦值.
所成的角的正弦值. 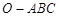 的侧棱
的侧棱 两两垂直,且
两两垂直,且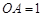 ,
,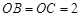 ,
,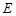 是
是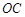 的中点。
的中点。
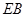 与
与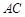 所成角的余弦值;
所成角的余弦值;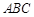 的所成角的正弦值。
的所成角的正弦值。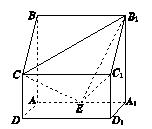
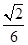 .求线段AM的长.
.求线段AM的长. 中,
中, 为
为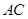 中点,
中点,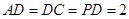 ,
,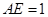 ,且
,且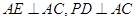 ,现沿
,现沿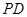 折起使
折起使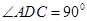 ,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.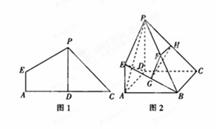
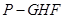 的体积;
的体积;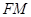 与直线
与直线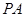 所成角为
所成角为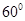 ?若存在,求出线段的长;若不存在,请说明理由.
?若存在,求出线段的长;若不存在,请说明理由.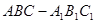 的侧面
的侧面 是菱形,
是菱形, ,D是
,D是 的中点,证明:
的中点,证明: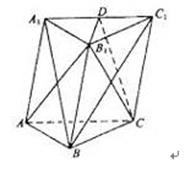
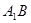 ∥面
∥面
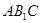
 平面
平面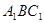 .
.