题目内容
设p:函数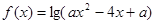
的定义域为R; q:不等式
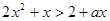,对
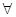
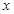∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数
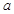的取值范围.
【答案】
【解析】
试题分析：先由函数定义域及不等式的恒成立条件可得
中的
的范围，然后由复合命题的真假判断得出.
试题解析：
且
，
，
恒成立，增函数
此时
，故
命题“p∨q”为真命题,命题“p∧q”为假命题,等价于一真一假，故.
考点：1.函数的定义域；2.不等式的恒成立问题；3.复合命题的真假判断
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
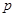：关于
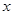的方程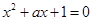
无实根；命题
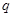：函数
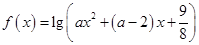的定义域为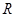
，若命题"p或q”是真命题，“p且q”是假命题，求实数a的取值范围．
的定义域为R;命题q:
对一切的实数均成立，如果命题“p或q”为真命题，且“p且q”为假命题，求实数a的取值范围。
的定义域为R;
不等式
恒成立
”为真命题，且“
”为假命题，求实数
的取值范围
的定义域为R; 
不等式
恒成立；
”为真命题，且“
”为假命题，求实数
的取值范围．