题目内容
【题目】已知数列![]() 是公差不为0的等差数列,
是公差不为0的等差数列,![]() ,数列
,数列![]() 是等比数列,且
是等比数列,且![]() ,
,![]() ,
,![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设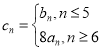 ,求
,求![]() 的前n项和
的前n项和![]() ;
;
(3)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)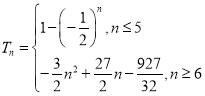 ;(3)
;(3)![]()
【解析】
(1)设等差数列![]() 的公差为
的公差为![]() ,等比数列
,等比数列![]() 的公比为
的公比为![]() ,根据
,根据![]() ,
,![]() ,
,![]() ,列方程组解方程组可得;
,列方程组解方程组可得;
(2)分![]() 和
和![]() 讨论,求
讨论,求![]() ;
;
(3)令![]() ,由单调性可得
,由单调性可得![]() ,由题意可得
,由题意可得![]() ,易得
,易得![]() 的最小值.
的最小值.
解:(1)设等差数列![]() 的公差为
的公差为![]() ,等比数列
,等比数列![]() 的公比为
的公比为![]() ,
,
则由题意可得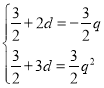 ,解得
,解得 或
或![]() ,
,
∵数列![]() 是公差不为0的等差数列,
是公差不为0的等差数列,![]() ,
,
∴数列![]() 的通项公式
的通项公式![]() ;
;
(2)由(1)知![]() ,
,
当![]() 时,
时,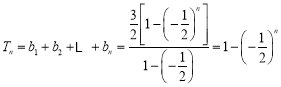 ,
,
当![]() 时,
时,
![]()
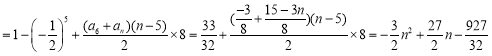 ,
,
综合得:
(3)由(1)可知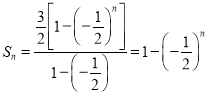 ,
,
令![]() ,
,![]() ,∴
,∴![]() 随着
随着![]() 的增大而增大,
的增大而增大,
当![]() 为奇数时,
为奇数时,![]() 在奇数集上单调递减,
在奇数集上单调递减,![]() ,
,
当![]() 为偶数时,
为偶数时,![]() 在偶数集上单调递增,
在偶数集上单调递增,![]() ,
,![]() ,
,
![]() 对
对![]() 恒成立,
恒成立,![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目