题目内容
17.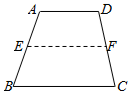 如图,梯形ABCD中,点E、F分别在AB、CD上,EF∥AD,假设EF作上下平行移动.
如图,梯形ABCD中,点E、F分别在AB、CD上,EF∥AD,假设EF作上下平行移动.(1)如果$\frac{AE}{EB}$=$\frac{1}{2}$,求证:3EF=BC+2AD;
(2)如果$\frac{AE}{EB}$=$\frac{2}{3}$,求证:5EF=2BC+3AD.
分析 (1)可分别延长BA,CD,且交于O点,可设OA=x,AE=y,EB=2y,根据条件中的平行关系便可得到$\frac{x}{x+y}=\frac{AD}{EF}$①,$\frac{x}{x+3y}=\frac{AD}{BC}$②,这样①②联立可消去y得到(3EF-2AD-BC)•x=0,从而便可得出3EF=BC+2AD;
(2)证明方法同(1),可设AE=2y,EB=3y,根据平行关系便可得出两个关于x,y的等式,消去y即可得出5EF=2BC+3AD.
解答 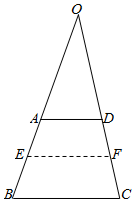 证明:如图,分别延长BA,CD,设交于O点,设OA=x;
证明:如图,分别延长BA,CD,设交于O点,设OA=x;
(1)如果$\frac{AE}{EB}=\frac{1}{2}$,设AE=y,EB=2y;
∵AD∥EF;
∴$\frac{x}{x+y}=\frac{AD}{EF}$①;
∵AD∥BC;
∴$\frac{x}{x+3y}=\frac{AD}{BC}$②;
①②联立消去y得,(3EF-2AD-BC)•x=0;
∴3EF-2AD-BC=0;
∴3EF=BC+2AD;
(2)如果$\frac{AE}{EB}=\frac{2}{3}$,设AE=2y,EB=3y;
∵AD∥EF;
∴$\frac{x}{x+2y}=\frac{AD}{EF}$③;
∵AD∥BC;
∴$\frac{x}{x+5y}=\frac{AD}{BC}$④;
③④联立消去y得,(5EF-3AD-2BC)•x=0;
∴5EF=2BC+3AD.
点评 考查平行线分线段成比例定理,以及相似三角形的判定,相似三角形的对应边的比例关系,消元法解二元一次方程的方法.

练习册系列答案
相关题目
7.cos(-$\frac{55}{6}$π)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
5.已知集合M={0,i}(i是虚数单位),集合N={x|x2+1=0,x∈C},则集合M∪N=( )
| A. | i | B. | {i} | C. | {0,i} | D. | {-i,0,i} |
12.命题“?a∈R,函数y=π”是增函数的否定是( )
| A. | “?a∈R,函数y=π”是减函数 | B. | “?a∈R,函数y=π”不是增函数 | ||
| C. | “?a∈R,函数y=π”不是增函数 | D. | “?a∈R,函数y=π”是减函数 |
9.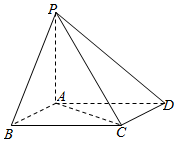 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )
 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )| A. | [$\frac{\sqrt{2}}{6}$,$\frac{1}{3}$) | B. | ($\frac{\sqrt{2}}{12}$,$\frac{1}{6}$] | C. | ($\frac{\sqrt{2}}{6}$,$\frac{1}{3}$] | D. | [$\frac{\sqrt{2}}{12}$,$\frac{1}{6}$) |
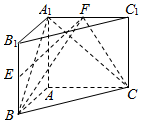 如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点.