题目内容
过抛物线x2=2py(p>0)的焦点F做倾斜角为30°的直线,与抛物线交于A、B两点(点A在y轴左侧),则 的值为( )
的值为( )A.3
B.

C.1
D.

【答案】分析:设出直线方程代入抛物线方程,求出A、B两点坐标,利用抛物线定义,即可得到结论.
解答:解:设直线l的方程为:x=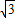 (y-
(y-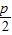 ),设A(x1,y1),B(x2,y2),
),设A(x1,y1),B(x2,y2),
将直线方程代入抛物线方程,消去x可得12y2-20py+3p2=0,
解方程得y1=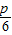 ,y2=
,y2=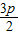
由抛物线的性质知,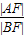 =
=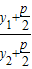 =
=
故选B.
点评:本题考查抛物线的定义、标准方程,考查学生的计算能力,属于基础题.
解答:解:设直线l的方程为:x=
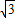 (y-
(y-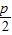 ),设A(x1,y1),B(x2,y2),
),设A(x1,y1),B(x2,y2),将直线方程代入抛物线方程,消去x可得12y2-20py+3p2=0,
解方程得y1=
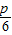 ,y2=
,y2=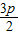
由抛物线的性质知,
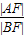 =
=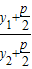 =
=
故选B.
点评:本题考查抛物线的定义、标准方程,考查学生的计算能力,属于基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
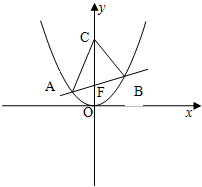 设直线l过抛物线x2=2py(p>0)的焦点F,且与该抛物线交于A、B两点,l的斜率为k,点C(0,t),当k=0,t=1+2
设直线l过抛物线x2=2py(p>0)的焦点F,且与该抛物线交于A、B两点,l的斜率为k,点C(0,t),当k=0,t=1+2