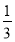题目内容
6. 在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,∠A=120°,BD=3.
在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,∠A=120°,BD=3.(1)求AD的长;
(2)若∠BCD=105°,求四边形ABCD的面积.
分析 (1)由余弦定理得能求出AD的长.
(2)由正弦定理得$\frac{BC}{sin45°}=\frac{DC}{sin30°}=\frac{3}{sin105°}$,从而BC=3$\sqrt{3}-3$,DC=$\frac{3\sqrt{6}-3\sqrt{2}}{2}$,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F,则AE=$\frac{1}{2}AB$=$\frac{\sqrt{3}}{2}$,CF=$\frac{1}{2}BC=\frac{3\sqrt{3}-3}{2}$,四边形ABCD的面积:S=S△ABD+S△BDC=$\frac{1}{2}×BD×(AE+CF)$,由此能求出结果.
解答 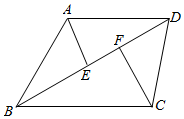 解:(1)∵在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,∠A=120°,BD=3.
解:(1)∵在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,∠A=120°,BD=3.
∴由余弦定理得:cos120°=$\frac{3+A{D}^{2}-9}{2×\sqrt{3}×AD}$,
解得AD=$\sqrt{3}$(舍去AD=-2$\sqrt{3}$),
∴AD的长为$\sqrt{3}$.
(2)∵AD∥BC,AB=$\sqrt{3}$,∠A=120°,BD=3,AD=$\sqrt{3}$,
∠BCD=105°,
∴∠DBC=30°,∠BDC=45°,
∴$\frac{BC}{sin45°}=\frac{DC}{sin30°}=\frac{3}{sin105°}$,
解得BC=3$\sqrt{3}-3$,DC=$\frac{3\sqrt{6}-3\sqrt{2}}{2}$,
如图,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F,
则AE=$\frac{1}{2}AB$=$\frac{\sqrt{3}}{2}$,CF=$\frac{1}{2}BC=\frac{3\sqrt{3}-3}{2}$,
∴四边形ABCD的面积:
S=S△ABD+S△BDC=$\frac{1}{2}×BD×(AE+CF)$
=$\frac{1}{2}×3×(\frac{\sqrt{3}}{2}+\frac{3\sqrt{3}-3}{2})$
=$\frac{12\sqrt{3}-9}{4}$.
点评 本题考查三角形的边长的求法,考查四边形的面积的求法,考查余弦定理、正弦定理、三角形性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

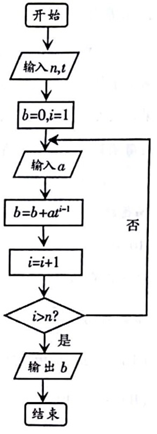 在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )
在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )| A. | 179 | B. | 178 | C. | 147 | D. | 146 |
| A. | 4π | B. | 8π | C. | 16π | D. | 9π |
| A. | -e | B. | 2 | C. | -2 | D. | $\frac{1}{e}$ |
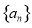 的前
的前 项和为
项和为 ,且
,且 ,在区间
,在区间 内任取一个实数作为数列
内任取一个实数作为数列 的最小值为
的最小值为 的概率为( )
的概率为( ) B.
B.  C.
C. 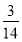 D.
D.