题目内容
设集合A={-1,2},B={x|x2-(a+1)x+a2-2=0},A∩B={2}
(Ⅰ)求集合B;
(Ⅱ)设全集U={-1,0,1,2,3,4},若集合M满足{-1}⊆M?∁UB,写出满足条件的所有集合M.
(Ⅰ)求集合B;
(Ⅱ)设全集U={-1,0,1,2,3,4},若集合M满足{-1}⊆M?∁UB,写出满足条件的所有集合M.
考点:集合的包含关系判断及应用
专题:集合
分析:根据交集的定义,由条件能得出2时集合B的元素,所以2是方程x2-(a+1)x+a2-2=0的解,带入方程便能求出a,这里要注意的是求得a之后,要验证是否符合条件.第二问,先求出∁∪B={-1,0,3,4},根据{-1}⊆M?∁UB知道M中必须含元素-1,或者含有0,3,4三个元素中的一个或两个,这样就能找出集合M.
解答:
解:(I)∵A∩B={2},∴2∈B,
代入B中的方程,得a2-2a=0,得a=0或a=2
当a=0时,B={-1,2},不满足条件,舍去;
当a=2时,B={1,2},满足条件.
综上,B={1,2}
(II)∵U={-1,0,1,2,3,4}∴CUB={-1,0,3,4}
所以 {-1}⊆M?{-1,0,3,4}
所以满足条件的所有集合M有{-1}、{-1,0}、{-1,3}、{-1,4}、{-1,0,3}、{-1,0,4}、{-1,3,4}.
代入B中的方程,得a2-2a=0,得a=0或a=2
当a=0时,B={-1,2},不满足条件,舍去;
当a=2时,B={1,2},满足条件.
综上,B={1,2}
(II)∵U={-1,0,1,2,3,4}∴CUB={-1,0,3,4}
所以 {-1}⊆M?{-1,0,3,4}
所以满足条件的所有集合M有{-1}、{-1,0}、{-1,3}、{-1,4}、{-1,0,3}、{-1,0,4}、{-1,3,4}.
点评:考查交集、补集及子集、真子集的概念找的时候注意不漏就可以了,而第一问求出a之后不要忘了验证.

练习册系列答案
相关题目
已知数列{xn}满足xn+2=xn+1-xn(n∈N*),x1=1,x2=3,记S=x1+x2+…+xn,则下列结论正确的是( )
| A、x100=-1,S100=5 |
| B、x100=-3,S100=5 |
| C、x100=-3,S100=2 |
| D、x100=-1,S100=2 |
已知圆心为点C(4,7),并且在直线3x-4y+1=0上截得的弦长为8的圆的方程为( )
| A、(x-4)2+(y-7)2=5 |
| B、(x-4)2+(y-7)2=25 |
| C、(x-7)2+(y-4)2=5 |
| D、(x-7)2+(y-4)2=25 |
某市出租车起步价为5元(起步价内行驶里程为3km),以后每1km价为1.8元 (不足1km按1km计价),则乘坐出租车的费用y(元)与行驶的里程x(km)之间的函数图象大致为下列图中的( )
A、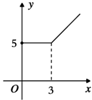 |
B、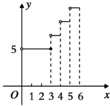 |
C、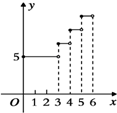 |
D、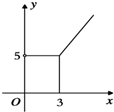 |
命题“若α=
,则sinα=1”的逆否命题是( )
| π |
| 2 |
A、若α≠
| ||
B、若α=
| ||
C、若sinα≠1,则α≠
| ||
D、若sinα≠1,则α=
|
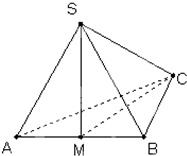 如图,在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
如图,在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2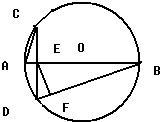 如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F.
如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F.