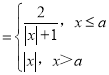题目内容
【题目】已知数列![]() 的首项
的首项![]() ,前
,前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)若数列![]() 为递增数列,求实数
为递增数列,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先根据已知等式得到![]() 和
和![]() 之间的关系,再根据递推关系得到从第二项起数列
之间的关系,再根据递推关系得到从第二项起数列![]() 的奇数项与数项与偶数项分别成等差数列,且公差为
的奇数项与数项与偶数项分别成等差数列,且公差为![]() ,进而得到数列
,进而得到数列![]() 为递增数列的条件,列出不等式组,解之可得实数
为递增数列的条件,列出不等式组,解之可得实数![]() 的取值范围;(2)结合(1)及错位相减减法求解即可.
的取值范围;(2)结合(1)及错位相减减法求解即可.
(1)由题意得,
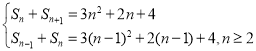 ,①
,①
则![]() ,②
,②
所以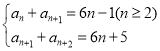 ,
,
所以![]() ,③
,③
所以从第二项起数列![]() 的奇数项与偶数项分别成等差数列,且公差为
的奇数项与偶数项分别成等差数列,且公差为![]() ,
,
令![]() ,由①式得
,由①式得![]() ,得
,得![]() ,
,
令![]() ,由②式得
,由②式得![]() ,得
,得![]() ,
,
令![]() ,由③式得
,由③式得![]() ,得
,得![]() ,
,
要使数列![]() 为递增数列,则
为递增数列,则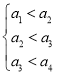 ,
,
即 ,解得
,解得![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(2)由(1)知,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
两式相减得,
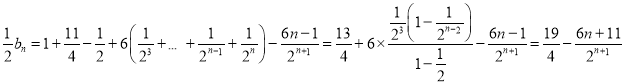 ,即
,即![]() ,
,
经检验,上式对![]() 也适用,故
也适用,故![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目