题目内容
13.在平面直角坐标系中,O为原点,A(1,0),B(2,2),若点C满足$\overrightarrow{OC}$=t($\overrightarrow{OB}$-$\overrightarrow{OA}$),t∈R,则点C的轨迹方程为( )| A. | 2x-y=0 | B. | 2x-y+2=0 | C. | 2x+y-2=0 | D. | 2x+y+2=0 |
分析 由向量等式,得点C的坐标,消去参数即得点C的轨迹方程.
解答 解:设C(x,y),则
由A(1,0),B(2,2),由点C满足$\overrightarrow{OC}$=t($\overrightarrow{OB}$-$\overrightarrow{OA}$),得
(x,y)=t(1,2),
∴$\left\{\begin{array}{l}{x=t}\\{y=2t}\end{array}\right.$,即点C的轨迹方程为2x-y=0.
故选:A.
点评 本题考查轨迹方程,考查向量知识的运用,确定坐标之间的关系是关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
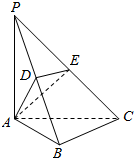 在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°,若AD⊥PB,垂足为D,AE⊥PC,垂足为E,求证:AD⊥PC.
在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°,若AD⊥PB,垂足为D,AE⊥PC,垂足为E,求证:AD⊥PC.