题目内容

在等腰△ABC中，AB=AC=1，向量
BA
与
AC
的夹角为60°，则向量
AB
在
CB
方向上的投影等于（　　）
分析：由向量
BA
与
AC
的夹角为60°，AB=AC，可得∠B=30°，利用投影的定义即可求解．
解答：解：根据题意：∵向量
BA
与
AC
的夹角为60°，∴∠A=120°，
∵AB=AC，∴∠B=30°
∴向量
AB
在
CB
方向上的投影等于|
AB
|•cos∠B=1•cos30°=
3
2

故选A．
点评：本题主要考查向量投影的定义及求解的方法，公式与定义两者要灵活运用．
练习册系列答案
相关题目
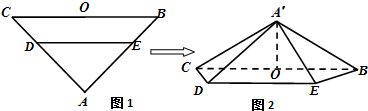如图1，在等腰△ABC中，∠A=90°，BC=6，D，E分别是AC，AB上的点，CD=BE=
2
，O为BC的中点．将△ADE沿DE折起，得到如图2所示的四棱锥A′-BCDE，其中A′O=
3
．
（1）证明：A′O⊥平面BCDE；      
（2）求A′D与平面A′BC所成角的正弦值．
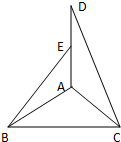如图，在等腰△ABC中，∠A=90°，BC=
2
，DA⊥AC，DA⊥AB，若DA=1，且E为DA的中点，求异面直线BE与CD所成角的余弦值．
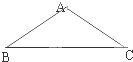如图，在等腰△ABC中，AB=AC=1，∠B=30°，则向量
AB
在向量
CA
上的投影等于（　　）
在三角形△ABC中，a，b，c分别是∠A，∠B，∠C的对应边，若asinA=bsinB，则三角形ABC是（　　）
如图1，在等腰△ABC中，∠A=90°，BC=6，D，E分别是AC，AB上的点，CD=BE=
2
，O为BC的中点．将△ADE沿DE折起，得到如图2所示的四棱锥A′-BCDE．若A′O⊥平面BCDE，则A′D与平面A′BC所成角的正弦值等于（　　）
精英家教网
A、
2
3
B、
3
3
C、
2
2
D、
2
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网