题目内容
已知动点M到点F .
.(1)求动点M的轨迹C的方程;
(2)若过点E(0,1)的直线与曲线C在y轴左侧交于不同的两点A、B,点P(-2,0)满足
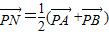 ,求直线PN在y轴上的截距d的取值范围..
,求直线PN在y轴上的截距d的取值范围..
【答案】分析:(1)直接设出点M的坐标,列出M的关系式,代入坐标化简即可.即用直接法求轨迹方程.
(2)由(1)可知动点M的轨迹C为双曲线,联立方程,消元,若过点E(0,1)的直线与曲线C在y轴左侧交于不同的两点A、B,即消元后的方程应有两个负实根,故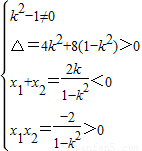 ,求出k的范围.由
,求出k的范围.由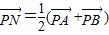 知N为AB的中点,由维达定理表示出N的坐标,写出PN的方程,令x=0,用k表示出直线PN在y轴上的截距d,转化为求函数的值域.
知N为AB的中点,由维达定理表示出N的坐标,写出PN的方程,令x=0,用k表示出直线PN在y轴上的截距d,转化为求函数的值域.
解答:解:(1)设动点M的坐标为(x,y),由题设可知 ,
,
∴动点M的轨迹C方程为x2-y2=1
(2)设A(x1,y1),B(x2,y2),
由题设直线AB的方程为:y=kx+1,
由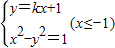 消去y得:(1-k2)x2-2kx-2=0(x≤-1),
消去y得:(1-k2)x2-2kx-2=0(x≤-1),
由题意可得: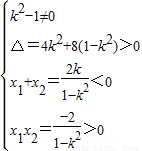
解得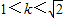 ∴
∴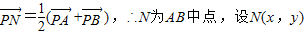
则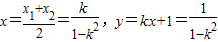 ,
,
∴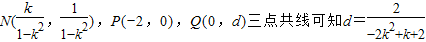
令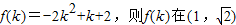 上为减函数.
上为减函数.
∴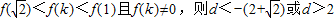 .
.
点评:本题考查直接法求轨迹方程和直线与双曲线位置关系的判断、圆锥曲线中范围的求解,综合性强,计算量大.
(2)由(1)可知动点M的轨迹C为双曲线,联立方程,消元,若过点E(0,1)的直线与曲线C在y轴左侧交于不同的两点A、B,即消元后的方程应有两个负实根,故
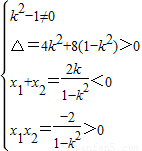 ,求出k的范围.由
,求出k的范围.由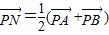 知N为AB的中点,由维达定理表示出N的坐标,写出PN的方程,令x=0,用k表示出直线PN在y轴上的截距d,转化为求函数的值域.
知N为AB的中点,由维达定理表示出N的坐标,写出PN的方程,令x=0,用k表示出直线PN在y轴上的截距d,转化为求函数的值域.解答:解:(1)设动点M的坐标为(x,y),由题设可知
 ,
,∴动点M的轨迹C方程为x2-y2=1
(2)设A(x1,y1),B(x2,y2),
由题设直线AB的方程为:y=kx+1,
由
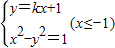 消去y得:(1-k2)x2-2kx-2=0(x≤-1),
消去y得:(1-k2)x2-2kx-2=0(x≤-1),由题意可得:
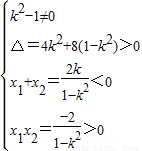
解得
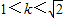 ∴
∴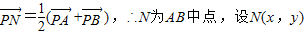
则
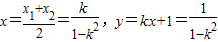 ,
,∴
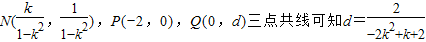
令
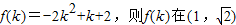 上为减函数.
上为减函数.∴
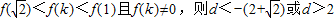 .
.点评:本题考查直接法求轨迹方程和直线与双曲线位置关系的判断、圆锥曲线中范围的求解,综合性强,计算量大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
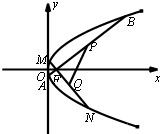 已知动点M到点F(1,0)的距离,等于它到直线x=-1的距离.
已知动点M到点F(1,0)的距离,等于它到直线x=-1的距离. (2013•深圳二模)已知动点 M 到点 F(0,1)的距离与到直线 y=4 的距离之和为 5.
(2013•深圳二模)已知动点 M 到点 F(0,1)的距离与到直线 y=4 的距离之和为 5.