题目内容
16.三棱锥P-ABC中,PA=PB=PC=4,BC=BA=2$\sqrt{2}$,BC⊥BA,P-ABC的各个顶点在一个球面上,则该球的表面积为$\frac{64π}{3}$.分析 求出AC=4,取AC中点O,连结PO,BO,则PO⊥AC,BO⊥AC,求出BO=2,PO=2$\sqrt{3}$,从而PO⊥平面ABC,在PD上取点D,连结BD,使BD=PD,则D为球心,由此能求出该球的表面积.
解答 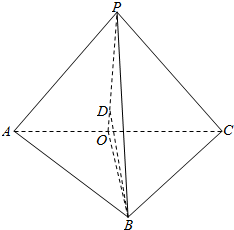 解:∵三棱锥P-ABC中,PA=PB=PC=4,BC=BA=2$\sqrt{2}$,BC⊥BA,
解:∵三棱锥P-ABC中,PA=PB=PC=4,BC=BA=2$\sqrt{2}$,BC⊥BA,
∴AC=$\sqrt{8+8}$=4,取AC中点O,连结PO,BO,则PO⊥AC,BO⊥AC,
BO=$\frac{1}{2}AC=2$,PO=$\sqrt{16-4}$=2$\sqrt{3}$,PO2+BO2=PB2,∴BO⊥BO,
∴PO⊥平面ABC,在PD上取点D,连结BD,使BD=PD,则D为球心,设球半径BD=PD=R,
∴R2=(2$\sqrt{3}$-R)2+22,
解得R=$\frac{4}{\sqrt{3}}$,
∴该球的表面积为S=4πR2=4π×($\frac{4}{\sqrt{3}}$)2=$\frac{64π}{3}$.
故答案为:$\frac{64π}{3}$.
点评 本题考查球的表面积的求法,是中档题,解题时要认真审题,注意四面体的结构特征和球的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目