题目内容
(本小题满分14分)
如图,在几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA⊥AB,M是EC的中点,EA=DA=AB=2CB.
(1)求证:DM⊥EB; (2)求异面直线AB与CE所成角的余弦值.
如图,在几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA⊥AB,M是EC的中点,EA=DA=AB=2CB.
(1)求证:DM⊥EB; (2)求异面直线AB与CE所成角的余弦值.
 |

解:以直线AE、AB、AD为x轴、y轴、z轴,建立空间直角坐标系A-xyz,
设CB=a,则A(0,0,0),E(2a,0,0),
B(0,2a,0),C(0,2a,a),D(0,0,2a),
所以M(a,a,0.5a), …………….2分
1)证: …….5分
…….5分
 ,
,
 ,即DM⊥EB. ………….8分
,即DM⊥EB. ………….8分
(2) ………….10分
………….10分
 c
c 
 .o. ………….12分m
.o. ………….12分m
∴异面直线AB与CE所成角的余弦值为 .o. ………….14分m
.o. ………….14分m
设CB=a,则A(0,0,0),E(2a,0,0),
B(0,2a,0),C(0,2a,a),D(0,0,2a),
所以M(a,a,0.5a), …………….2分
1)证:
 …….5分
…….5分 ,
,  ,即DM⊥EB. ………….8分
,即DM⊥EB. ………….8分 (2)
 ………….10分
………….10分 c
c 
 .o. ………….12分m
.o. ………….12分m ∴异面直线AB与CE所成角的余弦值为
 .o. ………….14分m
.o. ………….14分m
练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
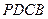 中,
中,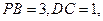
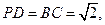
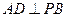
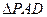 沿
沿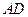 折起,使平面
折起,使平面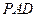 ⊥平面
⊥平面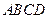 .
.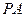 ⊥平面
⊥平面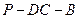 的大小;
的大小;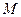 是侧棱
是侧棱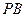 中点,求直线
中点,求直线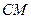 与平面
与平面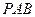 所成角的正弦值.
所成角的正弦值.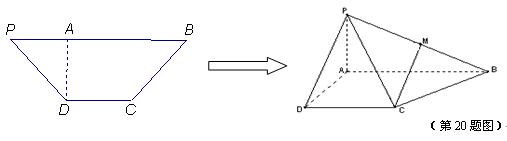
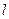 与曲线
与曲线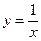 相切,分别求
相切,分别求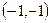 ;(2)
;(2)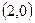 ;(3)
;(3)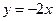 ;
;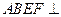 平面
平面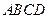 ,四边形
,四边形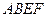 与
与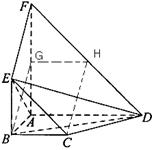
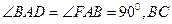
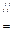
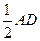 ,
,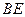
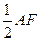 ,
,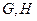 分别为
分别为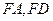 的中点
的中点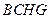 是平行四边形;
是平行四边形;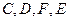 四点是否共面?为什么?
四点是否共面?为什么?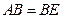 ,证明:平面
,证明:平面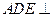 平面
平面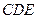 ;
;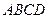 为矩形,
为矩形,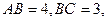 且
且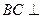 平面
平面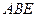 ,
,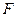 为
为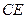 上的点,且
上的点,且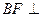 平面
平面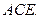
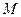 为线段
为线段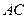 的中点,点
的中点,点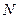 为线段
为线段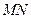 ∥平面
∥平面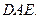

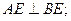
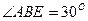 时,求三棱锥
时,求三棱锥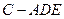 的体积。
的体积。
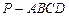 的底面为正方形,
的底面为正方形,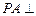 平面
平面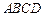 ,且
,且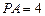 ,
,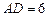 ,
,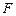 ,
,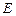 分别是线段
分别是线段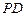 ,
,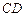 的中点.
的中点.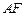 和
和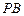 所成角的余弦值;
所成角的余弦值;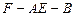 平面角的余弦值.
平面角的余弦值.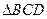 与
与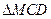 都是边长为2的正三角形,
都是边长为2的正三角形,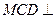 平面
平面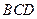 ,
,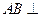 平面
平面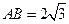 .
.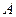 到平面
到平面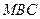 的距离;
的距离;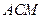 与平面
与平面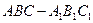 中,所有棱长均相等,
中,所有棱长均相等,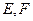 分别是棱
分别是棱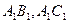 的中点,
的中点,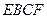 将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体.
将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体.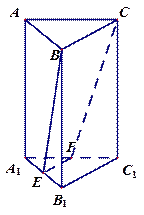 ①求几何体Ⅰ和几何体Ⅱ的表面积之比;
①求几何体Ⅰ和几何体Ⅱ的表面积之比; 内,则M、b、
内,则M、b、 b
b