题目内容
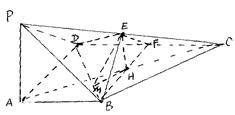
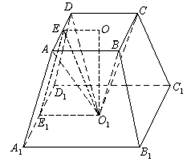
如图,在四棱锥P—ABCD中,PA⊥底面ABCD,∠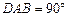 , AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
, AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
(Ⅰ)证明:CD⊥平面BEF;
(Ⅱ)设 ,
,
求k的值.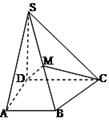
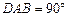 , AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
, AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.(Ⅰ)证明:CD⊥平面BEF;
(Ⅱ)设
 ,
,求k的值.

(Ⅰ)证明见解析(Ⅱ)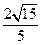
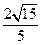
(Ⅰ)证明: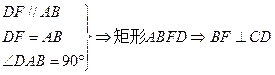 .………………………2分
.………………………2分
PA⊥平面ABCD,AD⊥CD. ……………………………………………3分
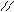
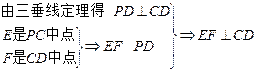 . ………………………………………5分
. ………………………………………5分
∴ CD⊥平面BEF. ……………………………………………………………………6分
(Ⅱ)连结AC且交BF于H,可知H是AC中点,连结EH,
由E是PC中点,得EH∥PA, PA⊥平面ABCD.
得EH⊥平面ABCD,且EH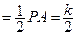 .…………………………………………8分
.…………………………………………8分
作HM⊥BD于M,连结EM,由三垂线定理可得EM⊥BD.
故∠EMH为二面角E—BD—F的平面角,故∠EMH=600.……………………10分
∵ Rt△HBM∽Rt△DBF,
 故
故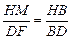 .
.
得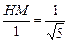 , 得
, 得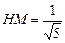 .
.
在Rt△EHM中,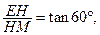
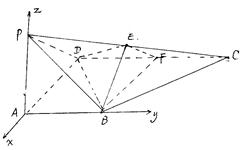 得
得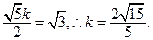 ………………………………………………………12分
………………………………………………………12分
解法2:(Ⅰ)证明,以A为原点,
建立如图空间直角坐标系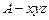 .
.
则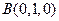 ,
,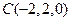 ,
,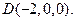
设PA = k,则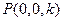 ,
,
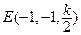 ,
,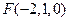 .………………………………………………………2分
.………………………………………………………2分
得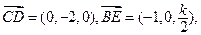
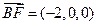 .…………………………4分
.…………………………4分
有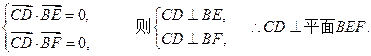 ………………6分
………………6分
(Ⅱ) …7分
…7分 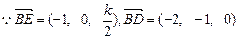 .
.
设平面BDE的一个法向量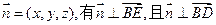 ,
,
则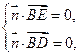 得
得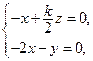 取
取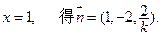 ……………10分 由
……………10分 由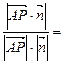
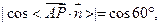 ………………………………………11分
………………………………………11分
得 …………………12分
…………………12分
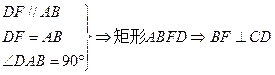 .………………………2分
.………………………2分PA⊥平面ABCD,AD⊥CD. ……………………………………………3分
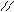
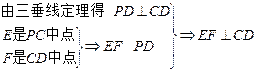 . ………………………………………5分
. ………………………………………5分∴ CD⊥平面BEF. ……………………………………………………………………6分
(Ⅱ)连结AC且交BF于H,可知H是AC中点,连结EH,
由E是PC中点,得EH∥PA, PA⊥平面ABCD.
得EH⊥平面ABCD,且EH
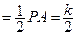 .…………………………………………8分
.…………………………………………8分作HM⊥BD于M,连结EM,由三垂线定理可得EM⊥BD.
故∠EMH为二面角E—BD—F的平面角,故∠EMH=600.……………………10分
∵ Rt△HBM∽Rt△DBF,
 故
故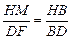 .
.得
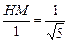 , 得
, 得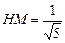 .
.在Rt△EHM中,
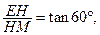
 得
得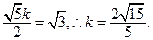 ………………………………………………………12分
………………………………………………………12分解法2:(Ⅰ)证明,以A为原点,
建立如图空间直角坐标系
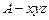 .
.则
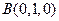 ,
,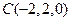 ,
,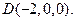
设PA = k,则
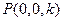 ,
,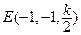 ,
,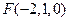 .………………………………………………………2分
.………………………………………………………2分得
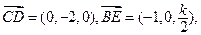
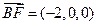 .…………………………4分
.…………………………4分有
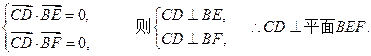 ………………6分
………………6分(Ⅱ)
 …7分
…7分 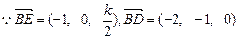 .
.设平面BDE的一个法向量
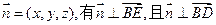 ,
,则
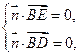 得
得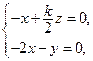 取
取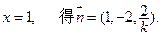 ……………10分 由
……………10分 由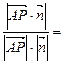
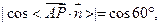 ………………………………………11分
………………………………………11分得
 …………………12分
…………………12分
练习册系列答案
相关题目
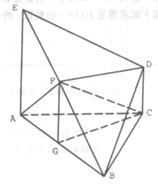
 的底面为直角梯形,
的底面为直角梯形, ,
, ,
, ,
, ,
, 底面
底面 ,
, 为
为 的中点.
的中点. 平面
平面 ;
; 与平面
与平面 所成的角;
所成的角; 到平面
到平面
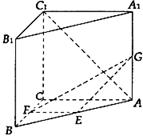
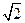 ,AC=3,BC=
,AC=3,BC=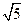 ,D是A1C的中点E是侧棱BB1上的一动点。
,D是A1C的中点E是侧棱BB1上的一动点。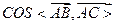 的值
的值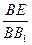 的值,不存在则说明理由。
的值,不存在则说明理由。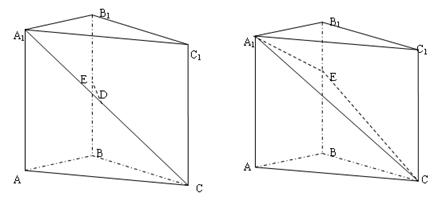
 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交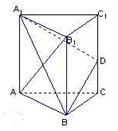
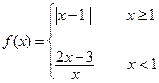 ,解不等式
,解不等式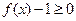 .
.