题目内容
6.已知函数f(x)的定义域为(0,+∞),当x∈(0,1)时f(x)>0,且x,y∈(0,+∞)时总有f(x•y)=f(x)+f(y)(1)求证:f($\frac{x}{y}$)=f(x)-f(y);
(2)证明:函数f(x)在定义域(0,+∞)上为减函数;
(3)若f(3)=1,且f(a)<f(a-1)+2,求a的取值范围.
分析 (1)需要特别注意构造方法,x=y•$\frac{x}{y}$即可.
(2)抽象函数的单调性证明需要特别注意构造方法,构造出$\frac{{x}_{1}}{{x}_{2}}$∈(0,1),可应用已知得f($\frac{{x}_{1}}{{x}_{2}}$)>0,进而根据函数单调性的定义得到结论.
(3)根据若f(3)=1,f(9)=2,根据运算法以及单调性求得a的范围.
解答 解:(1)证明:由题意得:
f(x)=f(y•$\frac{x}{y}$)=f(y)+f($\frac{x}{y}$),
故f($\frac{x}{y}$)=f(x)-f(y).
(2)证明:设0<x1<x2,
∴f(x1)=f(${x}_{2}•\frac{{x}_{1}}{{x}_{2}}$)=f(x2)+f($\frac{{x}_{1}}{{x}_{2}}$),
∵当x∈(0,1)时f(x)>0,
∵$\frac{{x}_{1}}{{x}_{2}}$∈(0,1),∴f($\frac{{x}_{1}}{{x}_{2}}$)>0,
∴f(x1)>f(x2),
∴函数f(x)在定义域(0,+∞)上为减函数;
(3)若f(3)=1,
∴f(9)=2,
∴f(a)<f(a-1)+f(9)=f(9(a-1)),
∴a>9(a-1),
∴1<a<$\frac{9}{8}$.
点评 本题考查抽象函数的运算法则以及单调性的证明和解不等式.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
17.下列说法正确的是( )
| A. | P(B|A)<P(AB) | B. | P(B|A)=$\frac{P(B)}{P(A)}$是可能的 | ||
| C. | 0<P(B|A)<1 | D. | P(A|A)=0 |
1.当行驶的6辆军车行驶至A处时,接上级紧急通知,这6辆军车需立即沿B、C两路分开纵队行驶,要求B、C每路至少2辆但不多于4辆.则这6辆军车不同的分开行驶方案总数是( )
| A. | 50 | B. | 1440 | C. | 720 | D. | 2160 |
15.已知函数f(x)=2x2+3,g(x)=a$\sqrt{{x}^{2}+1}$,若对于任意的x∈R,f(x)>g(x)恒成立,则实数a的取值范围是( )
| A. | (-∞,2$\sqrt{2}$) | B. | (-∞,2$\sqrt{2}$] | C. | (-∞,3) | D. | (-∞,3] |
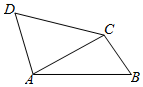 如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.
如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.