题目内容
已知f(x)=log2(1+x),g(x)=log2(1-x).
(1)求函数f(x)-g(x)的定义域;
(2)求使f(x)-g(x)>0的x的取值范围.
解:(1)由f(x)-g(x)=log2(1+x)-log2(1-x).得要使函数有意义,需
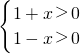 ,解得-1<x<1
,解得-1<x<1
∴函数f(x)-g(x)的定义域为(-1,1)
(2)f(x)-g(x)>0,即log2(1+x)-log2(1-x)>0.
即log2(1+x)>log2(1-x).
即 ,解得0<x<1
,解得0<x<1
故使f(x)-g(x)>0的x的取值范围为(0,1)
分析:(1)先写出函数f(x)-g(x)的解析式,利用对数函数的真数大于零,列不等式组即可解得函数的定义域;
(2)先将不等式转化为对数不等式,再利用对数函数的单调性和定义域列不等式组即可解得x的取值范围
点评:本题考查了函数的定义域的求法,对数函数的定义及其单调性,利用函数单调性解不等式的方法,转化化归的思想方法
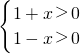 ,解得-1<x<1
,解得-1<x<1∴函数f(x)-g(x)的定义域为(-1,1)
(2)f(x)-g(x)>0,即log2(1+x)-log2(1-x)>0.
即log2(1+x)>log2(1-x).
即
 ,解得0<x<1
,解得0<x<1故使f(x)-g(x)>0的x的取值范围为(0,1)
分析:(1)先写出函数f(x)-g(x)的解析式,利用对数函数的真数大于零,列不等式组即可解得函数的定义域;
(2)先将不等式转化为对数不等式,再利用对数函数的单调性和定义域列不等式组即可解得x的取值范围
点评:本题考查了函数的定义域的求法,对数函数的定义及其单调性,利用函数单调性解不等式的方法,转化化归的思想方法

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log
x,那么f(-
)的值是( )
| 1 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |