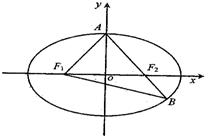
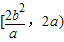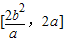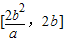题目内容
如图,已知椭圆方程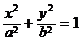 (a>b>0),焦点为F1,F2,P是椭圆上一点,∠F1PF2=α,求△F1PF2的面积(用a、b、α表示).
(a>b>0),焦点为F1,F2,P是椭圆上一点,∠F1PF2=α,求△F1PF2的面积(用a、b、α表示).
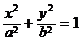 (a>b>0),焦点为F1,F2,P是椭圆上一点,∠F1PF2=α,求△F1PF2的面积(用a、b、α表示).
(a>b>0),焦点为F1,F2,P是椭圆上一点,∠F1PF2=α,求△F1PF2的面积(用a、b、α表示).
解:设P(x ,y) ,由椭圆的对称性,不妨设P 在第一象限,
由余弦定理知 |F1F2|2=|PF1|2+ |PF2|2-2|PF1| ·|PF2|cos α=4c2, ①
由椭圆定义知|PF1|+|PF2|=2a , ②
则②2- ①得|PF1| ·|PF2|=
故

由余弦定理知 |F1F2|2=|PF1|2+ |PF2|2-2|PF1| ·|PF2|cos α=4c2, ①
由椭圆定义知|PF1|+|PF2|=2a , ②
则②2- ①得|PF1| ·|PF2|=

故



练习册系列答案
相关题目
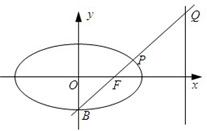 如图,已知椭圆C的方程为:
如图,已知椭圆C的方程为: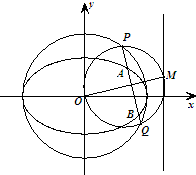 如图,已知椭圆方程为
如图,已知椭圆方程为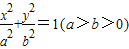 ,O为原点,点M是椭圆右准线上的动点,以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点,直线PQ与椭圆相交于A、B两点,则|AB|的取值范围是( )
,O为原点,点M是椭圆右准线上的动点,以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点,直线PQ与椭圆相交于A、B两点,则|AB|的取值范围是( )