题目内容
已知圆
及直线
，且
（1）证明无论m．n取什么实数，直线
与圆恒有公共点；
（2）求直线被圆截得的最短弦长及此时的直线的方程。
解：①由
得
∴直线l恒过定点A（3，1）
又因为圆C：
说明定点A（3，1）在圆C内部 ∴直线l与圆C恒有公共点。
②∵AC是圆C中经过A弦中最长的弦心距
∴当l⊥AC时，直线l被圆C截得的弦长BO最短A（3，1）C（1，2）
∴l被圆截得的最短弦长为
直线l的方程为：
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
与直线
及
都相切，且圆心在直线
上，则圆
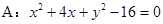及定点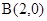
，点Q是圆A上的动点，点G在BQ上，点P在QA上，且满足
，
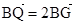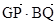=0．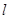
与曲线C交于M、N两点，直线
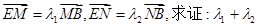为定值。
及直线
. 当直线
被圆
截得的弦长为
时, 求
的值, 并求过圆心
及直线
，且
与圆恒有公共点；