题目内容
(1)计算(
×
)6+(
)
-4(
)
-
×80.25-(-2014)0
(2)已知lg2=m,lg3=n,试用m,n表示log512..
| 3 | 2 |
| 3 |
2
|
| 4 |
| 3 |
| 16 |
| 49 |
| 1 |
| 2 |
| 4 | 2 |
(2)已知lg2=m,lg3=n,试用m,n表示log512..
考点:对数的运算性质,有理数指数幂的化简求值
专题:函数的性质及应用
分析:(1)利用根式和分数指数幂的性质和运算法则求解.
(2)利用对数的性质和运算法则求解.
(2)利用对数的性质和运算法则求解.
解答:
解:(1)(
×
)6+(
)
-4(
)
-
×80.25-(-2014)0
=22×33+(2
×
)
-4×(
)-1-2
×2
-1
=4×27+2-7-2-1
=100.
(2)∵lg2=m,lg3=n,
∴log512=
=
=
.
| 3 | 2 |
| 3 |
2
|
| 4 |
| 3 |
| 16 |
| 49 |
| 1 |
| 2 |
| 4 | 2 |
=22×33+(2
| 3 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 7 |
| 1 |
| 4 |
| 3 |
| 4 |
=4×27+2-7-2-1
=100.
(2)∵lg2=m,lg3=n,
∴log512=
| lg12 |
| lg5 |
| lg3+2lg2 |
| 1-lg2 |
| 2m+n |
| 1-m |
点评:本题考查指数和对数的化简求值,是基础题,解题时要认真审题,注意运算法则的合理运用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
设α为锐角,且cos(α+
)=
,则sin(α-
)的值为( )
| π |
| 3 |
| 4 |
| 5 |
| π |
| 6 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
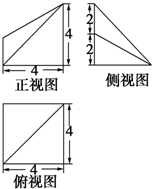 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
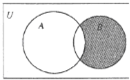 设区间U={1,2,3,4,5,6,7,8,9},集合A={1,2,3,5},B={2,4,6,7},则图中的阴影部分表示的集合为( )
设区间U={1,2,3,4,5,6,7,8,9},集合A={1,2,3,5},B={2,4,6,7},则图中的阴影部分表示的集合为( )| A、{2} |
| B、{4,6,7} |
| C、{1,2,5} |
| D、{4,6,7,8} |
正弦定理是指( )
| A、a=sinA | ||||||
| B、b=sinB | ||||||
| C、c=sinC | ||||||
D、
|
下列选项的对象中能构成集合的为( )
| A、一切很大的数 |
| B、聪明人 |
| C、正三角形的全体 |
| D、高一教材中的所有难题 |