题目内容
已知二次函数
在
处取得极值，且在
点处的切线与直线
平行．
(1）求
的解析式；
(2）求函数
的单调递增区间及极值。
（3）求函数在
的最值。
试题解析： (1)由
,可得
. 由题设可得
即
解得
,
.所以
.-
(2)由题意得
,所以
.令
,得
,
. 
所以函数g（x）的单调递增区间为（﹣∞，
），（1，+∞）．在x2=1有极小值为0． 在
有极大值
．------------------10分
（3）∵g（0）=0，g（2）=2，
∴由（2）知：函数g（x）的最大值为2，最小值为0．---------13分
练习册系列答案
相关题目
，则
＋
＋ 
<f(n) (n≥2，
)的过程中，由n＝k变到n＝k＋1时，左边增加了( )
项 D．
项已知函数
的定义域为
，部分对应值如下表, 的导函数
的图象如图所示. 下列关于的命题：
|
| －1 | 0 | 4 | 5 |
|
| 1 | 2 | 2 | 1 |
①函数的极大值点为
，
；
②函数在
上是减函数；
③如果当
时，的最大值是2，那么
的最大值为4；
④函数
的零点个数可能为0、1、2、3、4个．其中正确命题的序号是 ．
C．2
合并
同类项后的项数是（ ）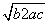
<
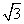a”索的因应是( )