题目内容
在正四面体S-ABC中,E为SA的中点,F为△ABC的中心,则异面直线EF与AB所成的角是________.
60°.
分析:根据正四面体S-ABC的特点求出其高以及底边的高,建立空间直角坐标系,写出各点的坐标,求出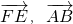 的坐标,利用向量的数量积公式求出
的坐标,利用向量的数量积公式求出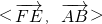 ,根据异面直线所成的角与向量角的关系求出答案.
,根据异面直线所成的角与向量角的关系求出答案.
解答:以SF为z轴,以FB为x轴建立空间直角坐标系,设正四面体S-ABC的棱长为1,则
△ABC的高为 ,
,
因为F为△ABC的中心,
所以根据三角形重心的性质,F到AC的距离为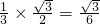 ,
,
所以A(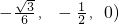 ,B(
,B(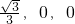 ),F(0,0,0)
),F(0,0,0)
在三角形SAF中,
SA=1,AF=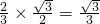 ,
,
所以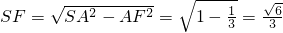 ,
,
所以S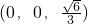 ,E(
,E(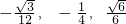 ),
),
所以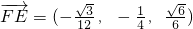 ,
,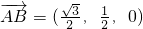 ,
,
所以cos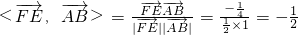
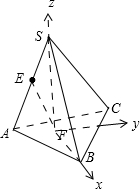
所以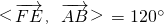 ,
,
所以异面直线EF与AB所成的角是60°.
故答案为60°.
点评:本题考查通过坐标系将立体几何问题转化为代数问题来解决,考查利用向量的数量积求异面直线所成的角,要注意异面直线所成角的范围.
分析:根据正四面体S-ABC的特点求出其高以及底边的高,建立空间直角坐标系,写出各点的坐标,求出
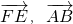 的坐标,利用向量的数量积公式求出
的坐标,利用向量的数量积公式求出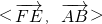 ,根据异面直线所成的角与向量角的关系求出答案.
,根据异面直线所成的角与向量角的关系求出答案.解答:以SF为z轴,以FB为x轴建立空间直角坐标系,设正四面体S-ABC的棱长为1,则
△ABC的高为
 ,
,因为F为△ABC的中心,
所以根据三角形重心的性质,F到AC的距离为
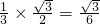 ,
,所以A(
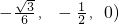 ,B(
,B(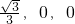 ),F(0,0,0)
),F(0,0,0)在三角形SAF中,
SA=1,AF=
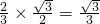 ,
,所以
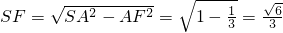 ,
,所以S
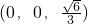 ,E(
,E(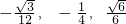 ),
),所以
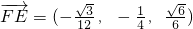 ,
,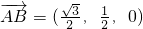 ,
,所以cos
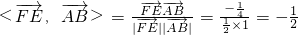
所以
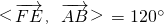 ,
,所以异面直线EF与AB所成的角是60°.
故答案为60°.

点评:本题考查通过坐标系将立体几何问题转化为代数问题来解决,考查利用向量的数量积求异面直线所成的角,要注意异面直线所成角的范围.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目




