题目内容
用二分法求函数
的一个零点，其参考数据如下：
|
|
|
|
|
|
|
|
据此数据，可得方程
的一个近似解（精确到0.01）为_________.
【答案】
1.56
【解析】解：由图表知，f（1.5625）=0.003＞0，f（1.5562）=-0.0029＜0，
∴函数f（x）=3x-x-4的一个零点在区间（1.5625，1.5562）上，
故函数的零点的近似值（精确到0.01）为 1.56，可得方程3x-x-4=0的一个近似解（精确到0.01）为 1.56，
故答案为 1.56．
练习册系列答案
相关题目
的一个正零点（误差不超过
）． 用二分法求函数
的一个零点，其参考数据如下：
| f(1.6000)=0.200 | f(1.5875)=0.133 | f(1.5750)=0.067 |
| f(1.5625)=0.003 | f(1.5562)=-0.029 | f(1.5500)=-0.060 |
据此数据，可得方程
的一个近似解（精确到0.01）为 ▲
的一个正实数零点，其参考数据如下：
的一个近似根（精确到0.1）为 ( )
的一个零点，根据参考数据，可得函数
的一个零点的近似解（精确到
）为（ ）（参考数据：
）
（B）
（C）
2.6 （D）
用二分法求函数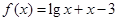
的一个零点，其参考数据如下：
|
f(2)≈-0.699 |
f(3) ≈0.477 |
f(2.5) ≈-0.102 |
f(2.75) ≈0.189 |
|
f(2.625) ≈0.044 |
f(2.5625)≈-0.029 |
f(2.59375)≈0.008 |
f(2.57813≈-0.011 |
根据此数据，可得方程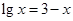
的一个近似解（精确到0.1）为