Question

在⊿ABC中，设，，，

（1）若⊿ABC为正三角形，求证：；

（2）若成立，⊿ABC是否为正三角形.

Answer 1

(1) 同解析，（2）⊿ABC是正三角形。

解析:

（1）设，则由与，与，与的夹角均为得：。

（2）若成立，则

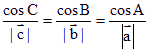∴，由正弦定理得。

两式两边分别相乘得，又∵，∴。

解法二：依题意有代入得

同理，所以三角形ABC是等边三角形。