题目内容

在△ABC中，设
AB
=
a
，
AC
=
b
，AP的中点为Q，BQ的中点为R，CR的中点为P，若
AP
=m
a
+n
b
，则m=
 
，n=
 
．
分析：由
AP
=m
a
+n
b
，利用中点关系得：
AQ
=
1
2
(m
a
+n
b
)，结合向量的减法的三角形法则得
BQ
=
AQ
-
AB
=
1
2
(m  
a
+n
b
)-
a
=(
1
2
m-1)
a
+
1
2
n
b
，同理得到得出：
AP
=
AC
+
CP
=(
1
8
m+
1
4
)
a
+(
1
8
n+
1
2
)
b
，
最后利用向量相等
AP
=m
a
+n
b
=(
1
8
m+
1
4
)
a
+(
1
8
n+
1
2
)
b
，列出m，n的方程组即可解得：m=
2
7
，n=
4
7
．
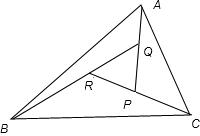解答：解：精英家教网由
AP
=m
a
+n
b
，得：
AQ
=
1
2
(m
a
+n
b
)，
∴
BQ
=
AQ
-
AB
=
1
2
(m  
a
+n
b
)-
a
=(
1
2
m-1)
a
+
1
2
n
b
，
∴
BR
=
1
2
[( 
1
2
m-1)
a
+
1
2
n
b
]=(
1
4
m-
1
2
)
a
+
1
4
n
b
，
由于：
CR
=
BR
-
BC
，
从而：
CR
=(
1
4
m+
1
2
)
a
+(
1
4
n-1)
b
，
∴
CP
=(
1
8
m+
1
4
)
a
+(
1
8
n-
1
2
)
b
，
从而得出：
AP
=
AC
+
CP
=(
1
8
m+
1
4
)
a
+(
1
8
n+
1
2
)
b
，
故有：
AP
=m
a
+n
b
=(
1
8
m+
1
4
)
a
+(
1
8
n+
1
2
)
b
，
∴
1
8
m+
1
4
=m
1
8
n+
1
2
=n

解得：m=
2
7
，n=
4
7

故答案为：
2
7
；
4
7
．
点评：本小题主要考查向量数乘的运算及其几何意义、向量加法减法的应用、向量相等的概念等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
在△ABC中，设
.
AB
=
.
a
，
.
AC
=
.
b
，点D在线段BC上，且
.
BD
=3
.
DC
，则
AD
用
a
，
b
表示为
 
．
如图，在△ABC中，设
AB
=a，
AC
=b，AP的中点为Q，BQ的中点为R，CR的中点恰为P．
（Ⅰ）若
AP
=λa+μb，求λ和μ的值；
（Ⅱ）以AB，AC为邻边，AP为对角线，作平行四边形ANPM，求平行四边形ANPM和三角形ABC的面积之比
S平行四边形ANPM
S△ABC
．
如图，在△ABC中，设
AB
=
a
，
AC
=
b
，AP的中点为Q，BQ的中点为R，CR的中点为P，若
AP
=m
a
+n
b
，则m+n=
6
7
6
7
．
精英家教网如图在△ABC中，设
AB
=
a
，
AC
=
b
，又
BD
=2
DC
，|
a
|=2，|
b
|=1，?
a
，
b
＞=
π
3
，（?
a
.
b
＞是表示向量
a
，
b
的夹角）
（1）用
a
，
b
表示
AD

（2）若点E是AC边的中点，直线BE交AD于F点，求
AF
•
AB
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网