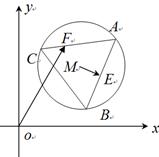
题目内容
已知圆内接正三角形，圆半径为2，假设在圆内随机撒一粒麦粒，则它落在正三角形内的概率为（ ）A．
B．
C．
D．
【答案】分析：由已知中半径为2的圆的正三角形ABC内接于圆O，我们可以计算出三角形ABC的面积及圆O的面积，代入几何概型公式，即可得到答案．
解答：
解：∵圆O是半径为R=2，圆O的面积为πR2=4π
则圆内接正三角形的边长为 2
，而正三角形ABC的面积为 
=3
，
∴豆子落在正三角形ABC内的概率P=
．
故选C．
点评：几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=N（A）/N求解．
解答：
解：∵圆O是半径为R=2，圆O的面积为πR2=4π则圆内接正三角形的边长为 2
，而正三角形ABC的面积为 =3，∴豆子落在正三角形ABC内的概率P=
．故选C．
点评：几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=N（A）/N求解．
练习册系列答案
相关题目
：
，
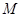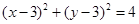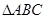为圆
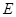为边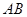
的中点，当正
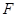在边
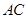上运动时，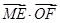
的最大值是 。 