题目内容
三棱锥P-ABC的侧棱PA，PB，PC两两互相垂直，且PA=PB=PC=2，则三棱锥P-ABC的外接球的体积是（ ）
A、2
| ||||
B、4
| ||||
C、
| ||||
D、8
|
考点：球的体积和表面积,球内接多面体
专题：计算题,空间位置关系与距离
分析：以PA、PB、PC为过同一顶点的三条棱，作长方体如图，则长方体的外接球同时也是三棱锥P-ABC外接球．算出长方体的对角线即为球直径，结合球的表面积公式，可算出三棱锥P-ABC外接球的体积．
解答：
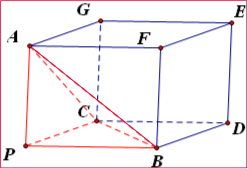解：以PA、PB、PC为过同一顶点的三条棱，作长方体如图
则长方体的外接球同时也是三棱锥P-ABC外接球．
∵长方体的对角线长为2
，
∴球直径为2
，半径R=
，
因此，三棱锥P-ABC外接球的体积是
πR3=
π×（
）3=4
π
故选：B．
解：以PA、PB、PC为过同一顶点的三条棱，作长方体如图则长方体的外接球同时也是三棱锥P-ABC外接球．
∵长方体的对角线长为2
| 3 |
∴球直径为2
| 3 |
| 3 |
因此，三棱锥P-ABC外接球的体积是
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
故选：B．
点评：本题给出三棱锥的三条侧棱两两垂直，求它的外接球的表面积，着重考查了长方体对角线公式和球的表面积计算等知识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知直线l1：ax+3y+1=0和直线l2：2x+（a+5）y+1=0平行，则a=（ ）
| A、1 | B、-6 | C、1或-6 | D、-3 |
已知m，n为异面直线，m?平面α，n?平面β，α∩β=l，则下面结论正确的为（ ）
| A、l与m，n都相交 |
| B、l与m，n中至少一条相交 |
| C、l与m，n都不相交 |
| D、l至多与m，n中的一条相交 |
在等比数列{an}中，a4=4，则a2•a6=（ ）
| A、32 | B、16 | C、8 | D、4 |
若sin（π-θ）＜0，tan（π+θ）＞0，则θ的终边在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |