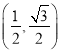[题目]已知椭圆上的点到两个焦点的距离之和为.短轴长为.直线与椭圆交于.两点.(1)求椭圆的方程, (2)若直线与圆相切.探究是否为定值.如果是定值.请求出该定值,如果不是定值.请说明理由．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知椭圆上的点到两个焦点的距离之和为，短轴长为，直线与椭圆交于、两点.

（1）求椭圆的方程；

（2）若直线与圆相切，探究是否为定值，如果是定值，请求出该定值；如果不是定值，请说明理由．

【答案】（1）（2）

【解析】试题分析：（1）由已知得由此能求出椭圆的方程．
（2）当直线轴时，．当直线与轴不垂直时，设直线直线与与圆的交点M（x1，y1），N（x2，y2），由直线与圆相切，得，联立，得（，由此能证明为定值．

试题解析：

1）由题意得

（2）当直线轴时，因为直线与圆相切，所以直线方程为

当时，得M、N两点坐标分别为，

当时，同理；

当与轴不垂直时，

设，由,

联立得

，， =

综上，（定值）

练习册系列答案

学习总动员单元复习专项复习期末复习系列答案

科目学生人数	A	B	C
120	是	否	是
60	否	否	是
70	是	是	否
50	是	是	是
150	否	是	是
50	是	否	否

（Ⅰ）试估计该校高三学生在A、B、C三门选修课中同时选修2门课的概率．

（Ⅱ）若该高三某学生已选修A，则该学生同时选修B、C中哪门的可能性大？

【题目】已知点在抛物线：的准线上，记的焦点为，过点且与轴垂直的直线与抛物线交于，两点，则线段的长为（）

A. 4 B. C. D.

【题目】从某校高三上学期期末数学考试成绩中，随机抽取了名学生的成绩得到如图所示的频率分布直方图：

（1）根据频率分布直方图，估计该校高三学生本次数学考试的平均分；

（2）若用分层抽样的方法从分数在和的学生中共抽取人，该人中成绩在的有几人？

（3）在（2）中抽取的人中，随机抽取人，求分数在和各人的概率．

【题目】已知椭圆方程，其左焦点、上顶点和左顶点分别为，，，坐标原点为，且线段，，的长度成等差数列．

（Ⅰ）求椭圆的离心率；

（Ⅱ）若过点的一条直线交椭圆于点，，交轴于点，使得线段被点，三等分，求直线的斜率．

【题目】如图，在四棱锥中，底面，底面是直角梯形，，，，是上的点．

（Ⅰ）求证：平面⊥平面；

（Ⅱ）若是的中点，且二面角的余弦值为，求直线与平面所成角的正弦值．

【题目】是否存在实数a，使得函数y=cos2x+asinx+ ﹣ 在闭区间[0，π]的最大值是0？若存在，求出对应的a的值；若不存在，试说明理由．

【题目】已知函数（）.

（1）写出函数的值域，单调区间（不必证明）；

（2）是否存在实数使得的定义域为，值域为？若存在，求出实数的取值范围；若不存在，请说明理由.

【题目】设在平面上有两个向量a=(cos 2α,sin 2α)(0≤α<π),b=,a与b不共线.

(1)求证:向量a+b与a-b垂直;

(2)当向量a+b与a-b的模相等时,求α的大小.

试题分类