题目内容
如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面![]() ,
,![]() ,AB=4,BC=3,
,AB=4,BC=3,![]() 是
是![]() 的中点,
的中点, ![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() ∥平面
∥平面![]() ;
;
(2)若Q为直线AP上任意一点,求几何体Q-BDE的体积;
(3)求平面DEF与平面ABCD所成角![]() 。
。

证明:(1)连结![]() 交
交![]() 与
与![]() ,连结
,连结![]() .
.
∵底面![]() 是正方形,∴点
是正方形,∴点![]() 是
是![]() 的中点.
的中点.
又∵![]() 是
是![]() 的中点∴在△
的中点∴在△![]() 中,
中,![]() 为中位线 ∴
为中位线 ∴![]() ∥
∥![]() .
.
而![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.
(2)![]() ∥平面
∥平面![]() ,
,![]()
(3)分别取CD、BD 的中点G、H,连EG、FH、GH
因为![]() 是
是![]() 的中点,
的中点, ![]() 为
为![]() 的中点,所以
的中点,所以![]() ∥PD,FH∥PD
∥PD,FH∥PD
![]()
![]()
![]()
![]() EF∥BC,GH∥BC,BC
EF∥BC,GH∥BC,BC![]() ,
,![]()
![]() ,GH
,GH![]() ,则EF⊥DE,GH⊥CD
,则EF⊥DE,GH⊥CD
 ,所以
,所以![]()
(另解:定义法,三垂线法![]() )
)

练习册系列答案
相关题目
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小. 中,底面
中,底面 是菱形,
是菱形, ,
, ,
, ,
, 平面
平面 是
是 的中点,
的中点, 是
是 的中点.
的中点.  ∥平面
∥平面 ;
; ;
; 所成的锐二面角的大小.
所成的锐二面角的大小.
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.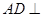 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小.
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, 为
为 中点,作
中点,作 交
交 于
于

 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。 中,底面
中,底面 为平行四边形,
为平行四边形, 平面
平面

 在棱
在棱 上.
上.
 时,求证
时,求证 平面
平面
 的大小为
的大小为 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.