题目内容
本小题满分12分)
已知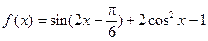
(Ⅰ)求函数f(x)的单调增区间
(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,且a=1,b+c=2,f(A)=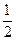 ,求△ABC的面积.
,求△ABC的面积.
已知
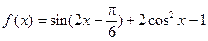
(Ⅰ)求函数f(x)的单调增区间
(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,且a=1,b+c=2,f(A)=
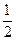 ,求△ABC的面积.
,求△ABC的面积.解:(Ⅰ)因为f(x)=
=
=
= ………………………………(3分)
………………………………(3分)
所以函数f(x)的单调递增区间是〔 〕(
〕( )……………(
)……………( 5分)
5分)
(Ⅱ)因为f(x)=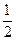 ,所以
,所以
又
从而 ……………………………………(7
……………………………………(7 分)
分)
在△ABC中,∵a=1,b+c=2,A=
∴1=b2+c2-2bccosA,即1=4-3bc.
故bc=1…………………………………………………………(10分)
从而S△ABC= ……………………………(12分)
……………………………(12分)

=

=

=
 ………………………………(3分)
………………………………(3分)所以函数f(x)的单调递增区间是〔
 〕(
〕( )……………(
)……………( 5分)
5分)(Ⅱ)因为f(x)=
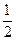 ,所以
,所以
又

从而
 ……………………………………(7
……………………………………(7 分)
分)在△ABC中,∵a=1,b+c=2,A=

∴1=b2+c2-2bccosA,即1=4-3bc.
故bc=1…………………………………………………………(10分)
从而S△ABC=
 ……………………………(12分)
……………………………(12分)略

练习册系列答案
相关题目
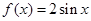 图象按向量
图象按向量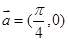 平移得函数
平移得函数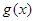 的图象,则函数
的图象,则函数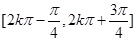 (
(  )
)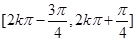 (
(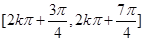 (
(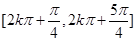 (
( 的图像关于( )对称。
的图像关于( )对称。


 ,
, .
. 时,求函数
时,求函数 的最大值;
的最大值; 上的任意一个
上的任意一个 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.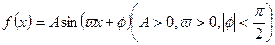 在一个周期内的部分函数图象如图所示.
在一个周期内的部分函数图象如图所示.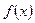 的解析式.
的解析式.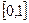 上的最大值和最小值.
上的最大值和最小值. BC中,a、b、c分别是角A、B、C的对边,
BC中,a、b、c分别是角A、B、C的对边,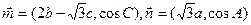 ,
,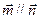 .
.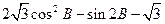 的取值区间。
的取值区间。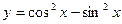 的周期是___________
的周期是___________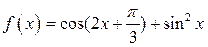
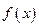 的最大值和最小正周期;
的最大值和最小正周期; 

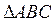 的三个内角,若
的三个内角,若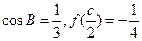 ,且C为锐角,求
,且C为锐角,求


 与
与 垂直,求
垂直,求 的值;
的值; 
 的最大值; (3)若
的最大值; (3)若 ,判断
,判断 是平行还是垂直.
是平行还是垂直.