题目内容
已知⊙O的直径为10,AB是⊙O的一条直径,长为20的线段MN的中点P在⊙O上运动(异于A、B两点).(Ⅰ)求证:
| AM |
| BN |
(Ⅱ)当
| MN |
| AB |
| AM |
| BN |
分析:(Ⅰ)由AB为⊙O的直径得
•
=0,利用向量的加法和减法运算来表示
•
,由向量数量积的运算和条件进行化简;
(Ⅱ)根据(Ⅰ)化简的结果和向量夹角的范围,求出夹角的余弦值的最大值代入,求出两个向量数量积的最大值.
| AP |
| BP |
| AM |
| BN |
(Ⅱ)根据(Ⅰ)化简的结果和向量夹角的范围,求出夹角的余弦值的最大值代入,求出两个向量数量积的最大值.
解答:证明:(Ⅰ)∵AB为⊙O的直径,P为圆上一点,∴AP⊥BP,
∴
⊥
,则
•
=0,
∵P为MN的中点,且|
|=20,∴
=
,
= |
|=10,
∴
•
=(
+
)(
+
)=(
-
)(
+
)
=
•
+
•
-
•
-
•
=
(
-
)-100=
•
-100,
∴
•
仅与
•
的夹角有关,而与点P在⊙O上的位置无关;
解:(Ⅱ)由(Ⅰ)得,
•
=
•
-100=100cosθ-100,
∵0≤θ<π,∴当θ=0时,
•
取最大值为0.
∴
| AP |
| BP |
| AP |
| BP |
∵P为MN的中点,且|
| MN |
| MP |
| PN |
| |MP| |
| PN |
∴
| AM |
| BN |
| AP |
| PM |
| BP |
| PN |
| AP |
| PN |
| BP |
| PN |
=
| AP |
| BP |
| AP |
| PN |
| PN |
| BP |
| PN |
| PN |
=
| PN |
| AP |
| BP |
| 1 |
| 2 |
| MN |
| AB |
∴
| AM |
| BN |
| MN |
| AB |
解:(Ⅱ)由(Ⅰ)得,
| AM |
| BN |
| 1 |
| 2 |
| MN |
| AB |
∵0≤θ<π,∴当θ=0时,
| AM |
| BN |
点评:本题考查了利用向量的线性运算和数量积运算,进行向量式子的求值和求解,主要根据图形的特点和条件进行转化,进而利用条件和夹角的范围求出式子的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 •
•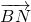 与点P在⊙O上的位置无关;
与点P在⊙O上的位置无关; 与
与 的夹角θ取何值时,
的夹角θ取何值时,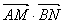 与点P在⊙O上的位置无关;
与点P在⊙O上的位置无关; 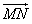 与
与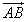 的夹角
的夹角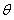 取何值时,
取何值时,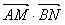 有最大值。
有最大值。  •
•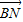 与点P在⊙O上的位置无关;
与点P在⊙O上的位置无关;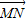 与
与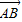 的夹角θ取何值时,
的夹角θ取何值时,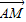 •
•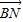 有最大值.
有最大值.